初中数学人教版八年级上册11.3.2 多边形的内角和表格教案设计

这是一份初中数学人教版八年级上册11.3.2 多边形的内角和表格教案设计，共4页。
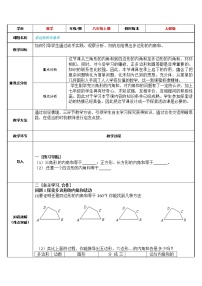
      学科数学年级/册八年级上册教材版本人教版课题名称第十一章   多边形的内角和难点名称探究多边形内角和公式时，如何将多边形分割成三角形难点分析从知识角度分析为什么难 多边形的内角和是本章的一个重点，是三角形有关知识的拓展，是以后学习平面镶嵌的基础，多边形内角和公式的运用还充分体现了图形与客观世界的联系。从学生角度分析为什么难学生好奇心比较强，观察能力、动手能力、探究能力都得到了一定的训练，但是把多边形转化为三角形这一过程是学生学习的难点 。难点教学方法启发学生尝试从不同的角度寻求解决问题的方法，并能有效地解决问题 教学环节教学过程导入温故知新：1.三角形内角和定理：三角形三个内角的和等于180°2.正方形，长方形每个内角都是90°，因此它们的内角和为360°思考：那任意四边形的内角和呢？是否为360°呢？  知识讲解（难点突破）探究新知：猜想：①任意四边形的内角和是多少？②如何把四边形的内角和转化为你所熟悉的问题？    类比四边形的内角和，你能算出五边形、六边形的内角和吗？如图：四边形ABCD可以分成  2  个三角形五边形ABCDE可以分成 3   个三角形六边形ABCDEF可以分成  4  个三角形n边形可以分成 （n-2） 个三角形多边形边数分成三角形个数多边形的内角和四边形22×180°五边形33×180°六边形44×180°………………n边形n-2（n-2）×180°         你能用其它方法将四边形分个三角形吗？尝试画出来成多（可提示学生在四边形内部取一点构造三角形）。     在四边形的内部找一个点与四个顶点连接，将四边形分成四个三角形，则四边形的内角和为：4×180°－360°= 360°五边形、六边形与六边形类似多边形边数分成三角形个数多边形的内角和四边形4180 °×4 -360°五边形5180  °×5-360°六边形6180 °×6 -360°………………n边形n180 °×n -360°          四边形除了上述分法，还可以怎么分？请尝试画出来！预设学生1：可以在四边形的一边上找一个点与四个顶点连接，将四边形分成三个三角形，则四边形的内角和为：3×180°－180°= 360°预设学生2：可以在四边形的外部找一个点与四个顶点连接，将四边形分成四个三角形，则四边形的内角和为：3×180°－180°= 360°回顾求四边形内角和的几种方法，发现：都是把四边形问题转化为熟悉的三角形问题来解决课堂练习（难点巩固） 求出下图中x的值（列式不带单位）     小结（1）将求多边形内角和转化求三角形的内角和，化未知为已知。（2）n边形的内角和等于(n-2)×180°，    多边形的内角和是180°的整数倍    多边形的边数增加1，内角和增加180º从特殊到一般