高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直备课课件ppt

这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直备课课件ppt，共29页。PPT课件主要包含了温故知新，面面垂直性质定理，面面垂直的综合应用，巩固练习，课堂总结等内容，欢迎下载使用。
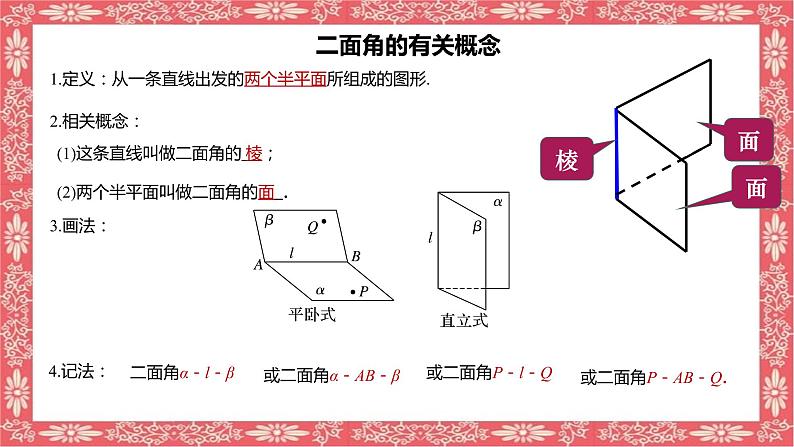
1.定义：从一条直线出发的两个半平面所组成的图形.
(1)这条直线叫做二面角的 棱；
(2)两个半平面叫做二面角的面 .
或二面角P－AB－Q.
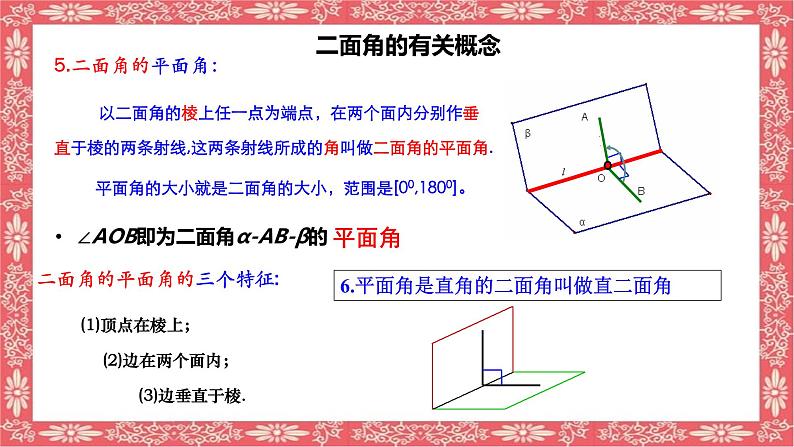
以二面角的棱上任一点为端点，在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
平面角的大小就是二面角的大小，范围是[00,1800]。
∠AOB即为二面角α-AB-β的
二面角的平面角的三个特征:
6.平面角是直角的二面角叫做直二面角
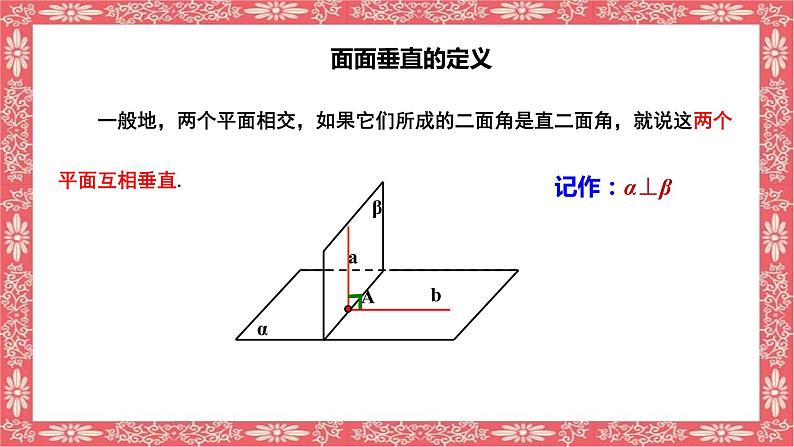
一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.
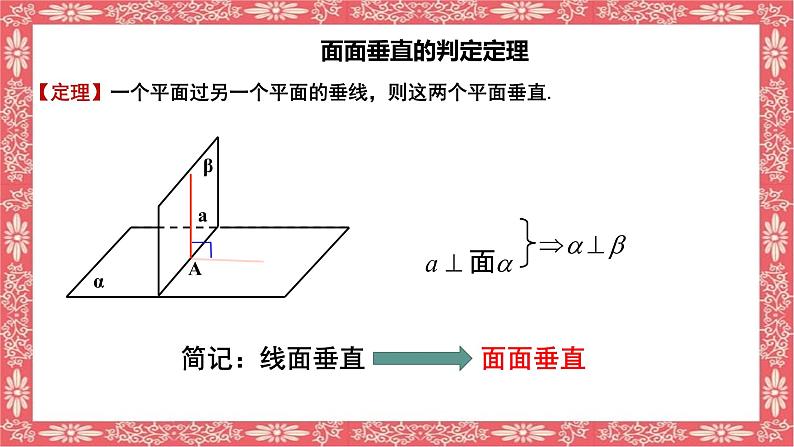
【定理】一个平面过另一个平面的垂线，则这两个平面垂直.
即是：在两个平面互相垂直的条件下，能推出哪些重要结论？
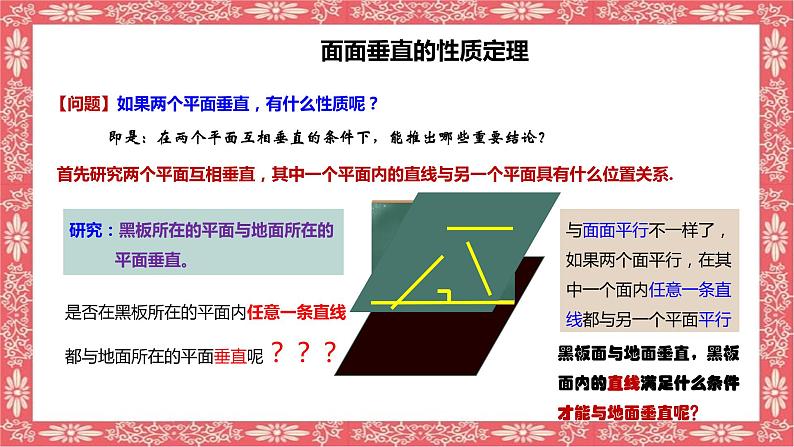
【问题】如果两个平面垂直，有什么性质呢？
首先研究两个平面互相垂直，其中一个平面内的直线与另一个平面具有什么位置关系.
是否在黑板所在的平面内任意一条直线都与地面所在的平面垂直呢？？？
研究：黑板所在的平面与地面所在的 平面垂直。
与面面平行不一样了，如果两个面平行，在其中一个面内任意一条直线都与另一个平面平行
黑板面与地面垂直，黑板面内的直线满足什么条件才能与地面垂直呢？
文字语言： 两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线 与另一个平面垂直.
面面垂直性质定理的应用
(2)若平面α⊥平面β，则平面α内所有直线都垂直于平面β.(　 　)
(4) 如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β（ ）.
(3)若平面α⊥平面β，则平面α内一定存在直线平行于平面β.(　 　)
面面垂直的性质定理的应用
(1)若平面α内的一条直线垂直于平面β内的任意一条直线，则α⊥β.(　 　)
例2：若平面α⊥平面β，平面β⊥平面γ，则(　　) A．α∥γ　　　　B．α⊥γ C．α与γ相交但不垂直 D．以上都有可能
例3：若平面α⊥平面β，且α∩β＝l，则下列命题中正确的个数是( ). (1) 平面α内的直线必垂直于平面β内的任意一条直线. (2) 平面α内的已知直线必垂直于平面β内的无数条直线. (3) 平面α内的任一条直线必垂直于平面β. (4) 过平面α内任意一点作交线l的垂线，则此垂线必垂直于平面β. (A) 3 (B) 2 (C) 1 (D) 0
例3：已知PA⊥平面ABC，平面PAB⊥平面PBC. 求证：BC⊥平面PAB.
证明：过点A作AD⊥PB，垂足为D.
∵平面PAB⊥平面PBC, 平面PAB∩平PBC=PB，
∵BC平面PBC，∴BC⊥AD.
又∵PA⊥平面ABC，BC平面ABC，∴BC⊥PA.
又PA∩AD=A，∴BC⊥平面PAB.
面面垂直的性质定理应用要注意以下三点
(2)直线必须在其 中一个平面内
(3)直线必须垂直 于它们的交线
证：如题图(1),在梯形ABCD中,AD＝CD＝2,∠ADC＝90°，
过C作CE⊥AB，E为垂足，∴四边形AECD为正方形，∴CE＝AE＝EB＝2，
∴∠ACE＝∠BCE＝45°，∴∠ACB＝90°即BC⊥AC，
如题图(2)，平面ACD⊥平面ABC且平面ACD∩平面ABC＝AC，
又BC⊂平面ABC且BC⊥AC，∴BC⊥平面ACD.
【问题】如果两个平面垂直，还有什么性质呢？
证: (1)取EF的中点N，连接MN，DN，MD. 根据题意可知，四边形ABFE是边长为2的正方形，又M，N分别为AB，EF的中点，
∴MN⊥平面CDEF.
又MN⊂平面ABFE，∴平面ABFE⊥平面CDEF.
∴MN⊥EF，MN＝2.
由(1)知MN⊥平面CDEF，又MN∥BF∥AE，∴BF⊥平面CDEF，AE⊥平面CDEF，
∴BF⊥CF，又CF⊥EF，BF∩EF＝F，∴CF⊥平面ABFE，
则V六面体ABCDEF＝V四棱锥C－ABFE＋V三棱锥A－CDE.
1：在三棱柱ABC-A1B1C1中，BC＝CC1，平面A1BC1⊥平面BCC1B1.证明：平面AB1C⊥平面A1BC1.
直线、平面之间位置关系的相互转化是立体几何中的重要思想方法.
1．面面垂直的性质定理
2．面面垂直的综合应用
课本P161 练习 1,2,3,4
课本P162 习题8.6 5,9,10