高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行授课课件ppt

这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行授课课件ppt，文件包含8531平面与平面平行pptx、8531平面与平面平行docx等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。
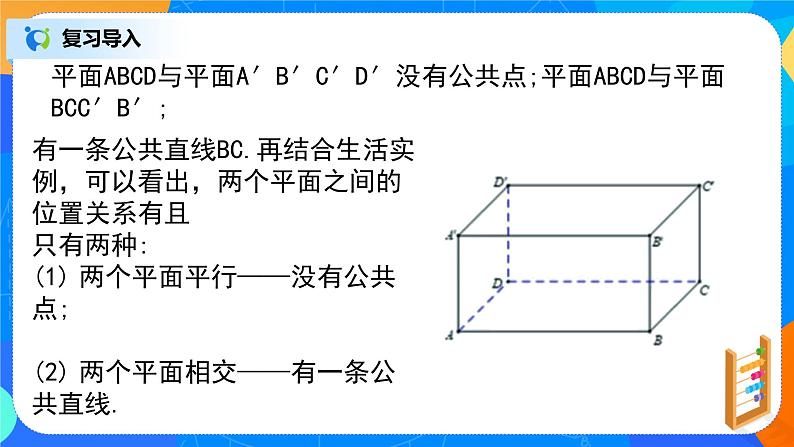
平面ABCD与平面A′B′C′D′没有公共点;平面ABCD与平面BCC′B′;
有一条公共直线BC.再结合生活实例，可以看出，两个平面之间的位置关系有且 只有两种: (1) 两个平面平行——没有公共点; (2) 两个平面相交——有一条公共直线.
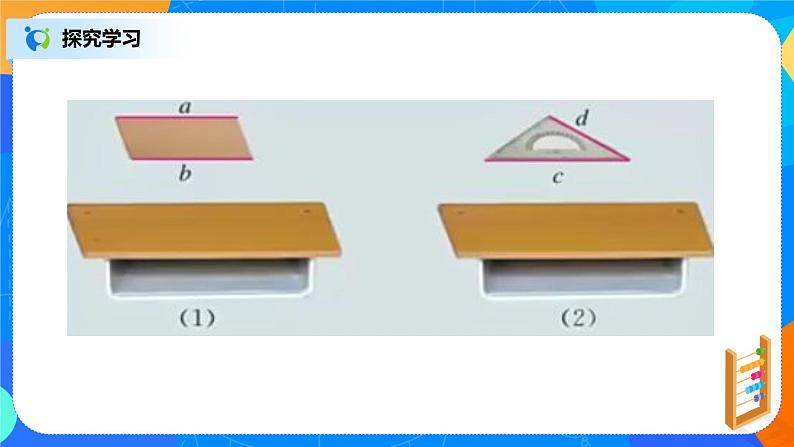
画两个互相平行的平面时，要注意使表示平面的两个平行四边形的对边平行.
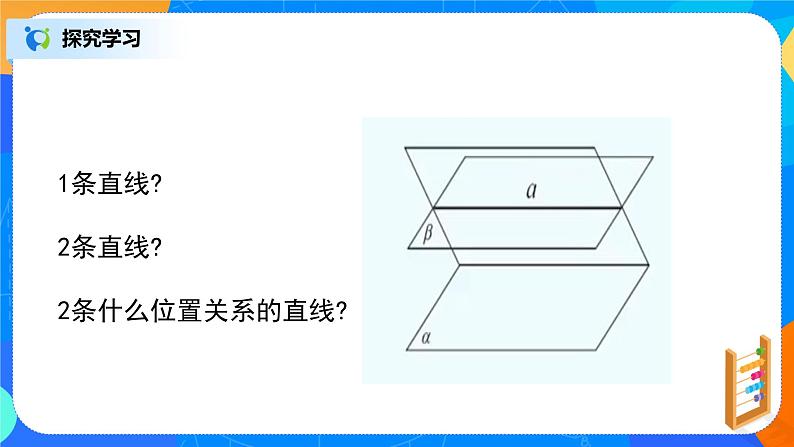
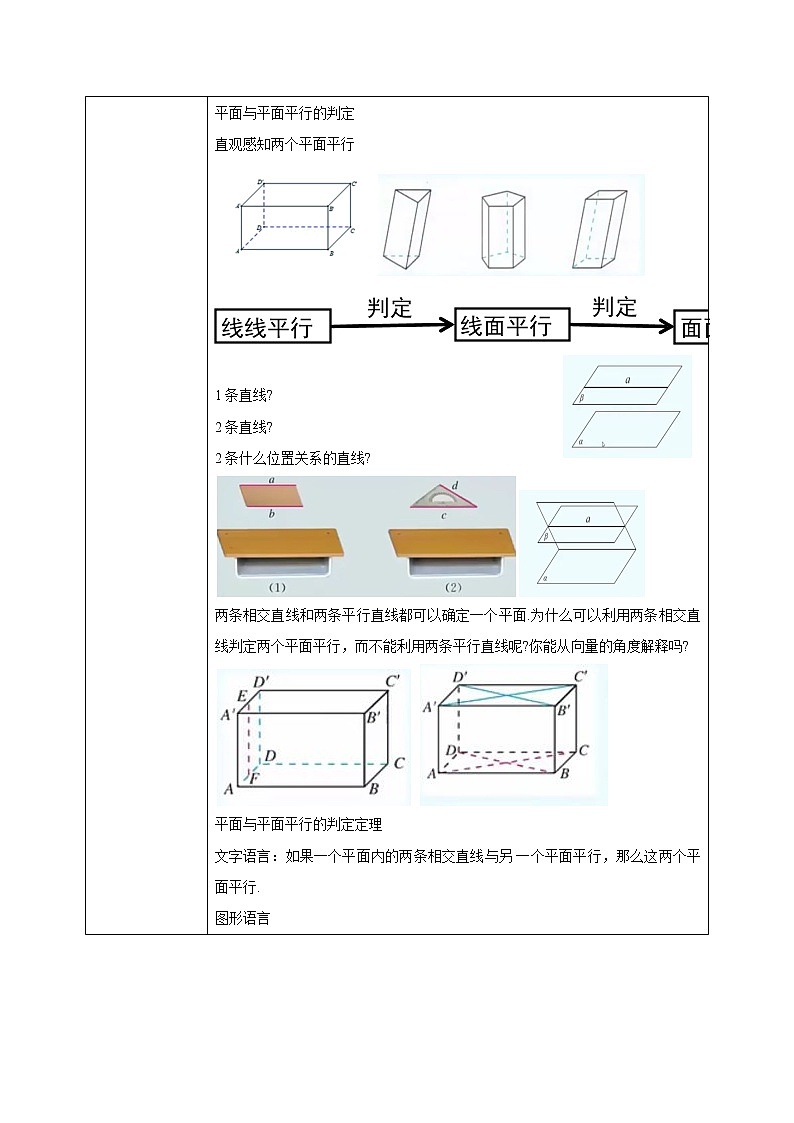
1条直线? 2条直线? 2条什么位置关系的直线?
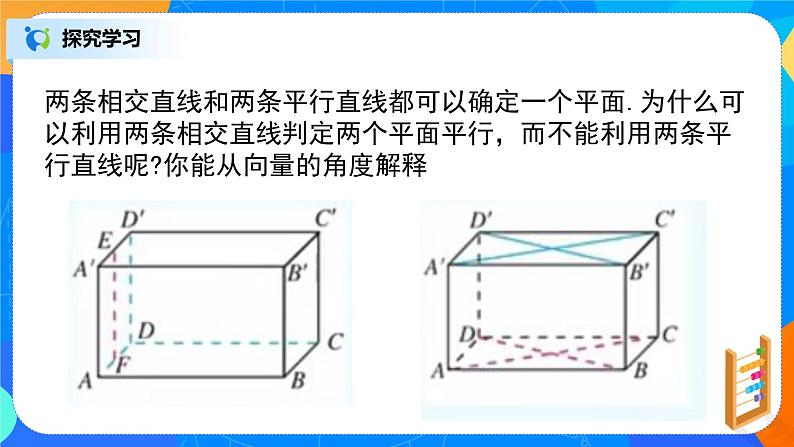
两条相交直线和两条平行直线都可以确定一个平面.为什么可以利用两条相交直线判定两个平面平行，而不能利用两条平行直线呢?你能从向量的角度解释
平面与平面平行的判定定理
文字语言：如果一个平面内的两条相交直线与另 一个平面平行，那么这两个平面平行. 图形语言
符号语言：a⊂ β，b⊂β，a∩b=P，a//α，b//α→α//β
已知：如图a⊂ β，b⊂β，a∩b=P，a//α，b//α 求证: α//β 证明:假设平面a与平面β不平行，设a∩β=c. 由a//α，a⊂ β则 a//c. 又由 b//α, b⊂ß, 则 b//c. 则 a//b. 与a∩b= P矛盾， 则α//β
判定平面与平面平行方法平面与平面平行的定义:平面与平面没有公共点 平面与平面平行的判定定理 利用判定定理证明两个平面平行，必须具备以下两个条件: (1) 平面内有两条直线平行于另一个平面;(2) 这两条直线必须相交. a⊂ β，b⊂β，a∩b=P，a//α，b//α→α//β
例1如图，已知正方体ABCD --A1B1C1D1, 求证:平面AB1D1//平面BC1D.
证明: 由ABCD-A1B1C1D1 为正方体， 则D1C1//A1B1, D1C1=A1B1, AB//A1B1，AB=A1B1. 即D1C1//AB, D1C1=AB, 即 D1C1BA为平行四边形. D1A// C1B. 又 D1A1⊄ 平面BC1D, CB⊂平面BC1D,
同理D1 B1//平面BC1D. 又 D1A1∩D1B1=D1 则平面AB1D1//平面BC1D.
例2如图， 已知三棱锥P-ABC中，D, E, F分别是PA, PB, PC的中点求证:平面DEF //平面ABC.
证明:在△PAB中，因为D,E分别是PA,PB的中点， 所以DE // AB. 又DE⊄平面ABC，AB⊂平面ABC, 因此DE//平面ABC. 同理,EF //平面ABC. 又因为DE∩EF=E, 所以平面DEF //平面ABC.