北师大版八年级下册2 直角三角形示范课课件ppt

这是一份北师大版八年级下册2 直角三角形示范课课件ppt，共26页。PPT课件主要包含了学习目标，情境导入，探索交流，证明欣赏，总统证法，∴a2+b2c2，a+b2，c2+，c2a2+b2，+b-a2等内容，欢迎下载使用。

1.复习直角三角形的相关知识，归纳并掌握直角三角形的性质和判定.2.学习并掌握勾股定理及其逆定理，能够运用其解决问题.（重点、难点）
直角三角形的两个锐角互余.
问题1 直角三角形的定义是什么？
问题2 三角形内角和的性质是什么？
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
这节课我们一起来证明直角三角形的判定与性质.
问题3 前面我们探究过直角三角形的哪些性质？
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°.
我们学过直角三角形的哪些性质和判定方法？与同伴交流.
性质：直角三角形有一个角是直角，两个锐角互余.
判定：有一个角是直角的三角形是直角三角形.
（1）直角三角形的两个锐角有怎样的关系？为什么？（2）如果一个三角形有两个角互余，那么这个三角形是直角三角形吗？为什么？
(1)根据三角形的内角和定理，即可得到“直角三角形的两锐角互余”.
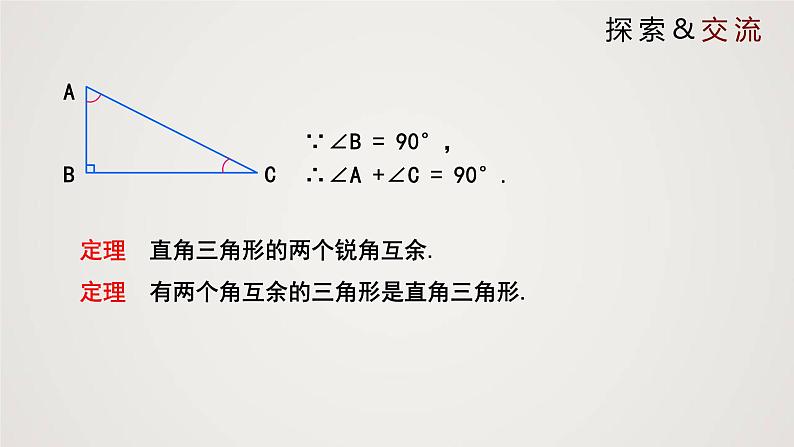
（2）如图，在△ABC中，∠A+∠B=90°，那么△ABC是直角三角形吗？
在△ABC中，因为∠A+∠B+∠C=180°，又∠A+∠B=90°，所以∠C=90°.于是△ABC是直角三角形.
定理 直角三角形的两个锐角互余.定理　有两个角互余的三角形是直角三角形.
∵∠B = 90°，∴∠A +∠C = 90°.
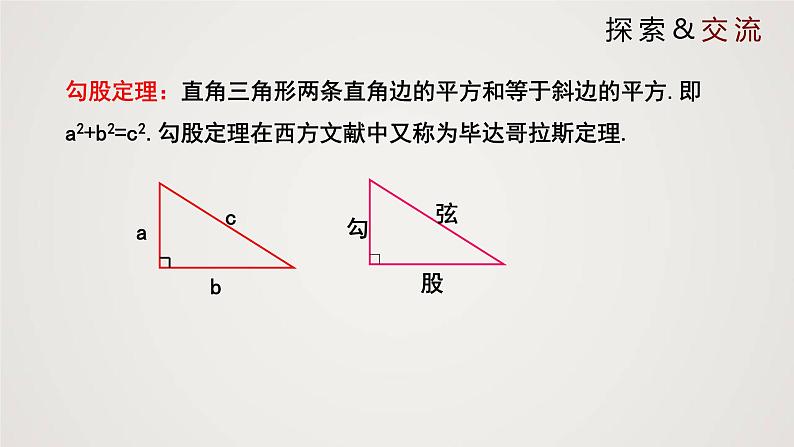
勾股定理：直角三角形两条直角边的平方和等于斜边的平方.即a2+b2=c2.勾股定理在西方文献中又称为毕达哥拉斯定理.
美国第20任总统：詹姆斯·艾伯拉姆·加菲尔德
∵ (a+b)2 = c2+ ，
a2+2ab+b2 = c2+2ab，
大正方形的面积可以表示为 ；也可以表示为 ；
2．利用正方形面积拼图证明：
∵ c2= +(b-a)2，
c2 =2ab+b2-2ab+a2，
∴ a2+b2=c2.
大正方形的面积可以表示为 ；也可以表示为　　　　 ．
例1.如图，在△ABC中，∠C＝70°，∠B＝30°，AD⊥BC于点D，AE为∠BAC的平分线，求∠DAE的度数．
解：由题意可知，∠BAC＝180°－∠B－∠C＝180°－30°－70°＝80°.∵AE为∠BAC的平分线，∴∠CAE＝∠BAE＝∠BAC＝40°.∵AD⊥BC，∴∠ADC＝90°.∴∠CAD＝90°－∠C＝90°－70°＝20°.∴∠DAE＝∠CAE－∠CAD＝40°－20°＝20°.
反过来，在一个三角形中，当两边的平方和等于第三边的平方时，我们曾用度量的方法得出“这个三角形是直角三角形”的结论．你能证明此结论吗？已知：如图 ，在△ABC中，AB2＋AC2＝BC2.求证：△ABC是直角三角形
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
证明：如图作 Rt△A'B'C'，
使∠A'=90°，A'B'=AB，A’C'=AC，
则 A'B'2+A'C'2 =B'C'2（勾股定理）
∵AB2+AC2=BC2，
∴BC2=B'C'2.
∴△ABC≌△A'B'C'（SSS）.
∴∠A=∠A'= 90°.
因此，△ABC是直角三角形.
定理 如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.
定理:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形．
勾股定理:直角三角形两条直角边的平方和等于斜边的平方．
下面两个定理的条件和结论有什么样的关系？
一个命题的条件和结论分别是另一个命题的结论和条件．
1.如果两个角是对顶角，那么它们相等；2.如果两个角相等，那么它们是对顶角.
3.如果小明患了肺炎，那么他一定会发烧；4.如果小明发烧，那么他一定患了肺炎.
5.一个三角形中相等的边所对的角相等；6.一个三角形中相等的角所对的边相等.
观察上面三组命题,你发现了什么?
在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题.
如果把其中一个命题叫做原命题，那么另一个命题就叫做它的逆命题.
上面每两个命题的条件和结论恰好互换了位置．
命题“两直线平行，内错角相等”的条件和结论为：条件为：两直线平行；结论为：内错角相等．因此它的逆命题为：
内错角相等，两直线平行.
你能写出命题“如果两个有理数相等，那么它们的平方相等”的逆命题吗？它们都是真命题吗？
逆命题：如果两个有理数的平方相等，那么这两个有理数相等.
原命题是真命题，逆命题是假命题.
如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，其中一个定理称为另一个定理的逆定理.
例2.举例说明下列命题的逆命题是假命题.
（2）如果两个角都是直角，那么这两个角相等.
逆命题：如果两个角相等，那么这两个角是直角.
例如10能被5整除，但它的个位数是0.
（1）如果一个整数的个位数字是5 ，那么这个整数能被5整除.
逆命题：如果一个整数能被5整除，那么这个整数的个位数字是5.
例如60°=60°，但这两个角不是直角.
1.下列命题中，属于假命题的是( )A.三角形三个内角的和等于180° B.两直线平行，同位角相等C.矩形的对角线相等 D.相等的角是对顶角
2.如图是一张直角三角形的纸片，两直角边AC＝6 cm，BC＝8 cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）
A.4 cm B.5 cm C.6 cm D.10 cm
3.如图所示，一场暴雨过后，垂直于地面的一棵树在距地面1米处折断，树尖B 恰好碰到地面，经测量AB=2米，则树高为 ( ) A. 米 B. 米 C.( +1)米 D.3 米
4. 如图，在四边形 ABCD 中，AB∥CD，E 为 BC 上的一点，且∠BAE=25°，∠CDE=65°，AE =2，DE=3，求 AD 的长.