2020-2021学年第10章 相交线、平行线和平移10.3 平行线的性质教案设计

这是一份2020-2021学年第10章 相交线、平行线和平移10.3 平行线的性质教案设计，共4页。
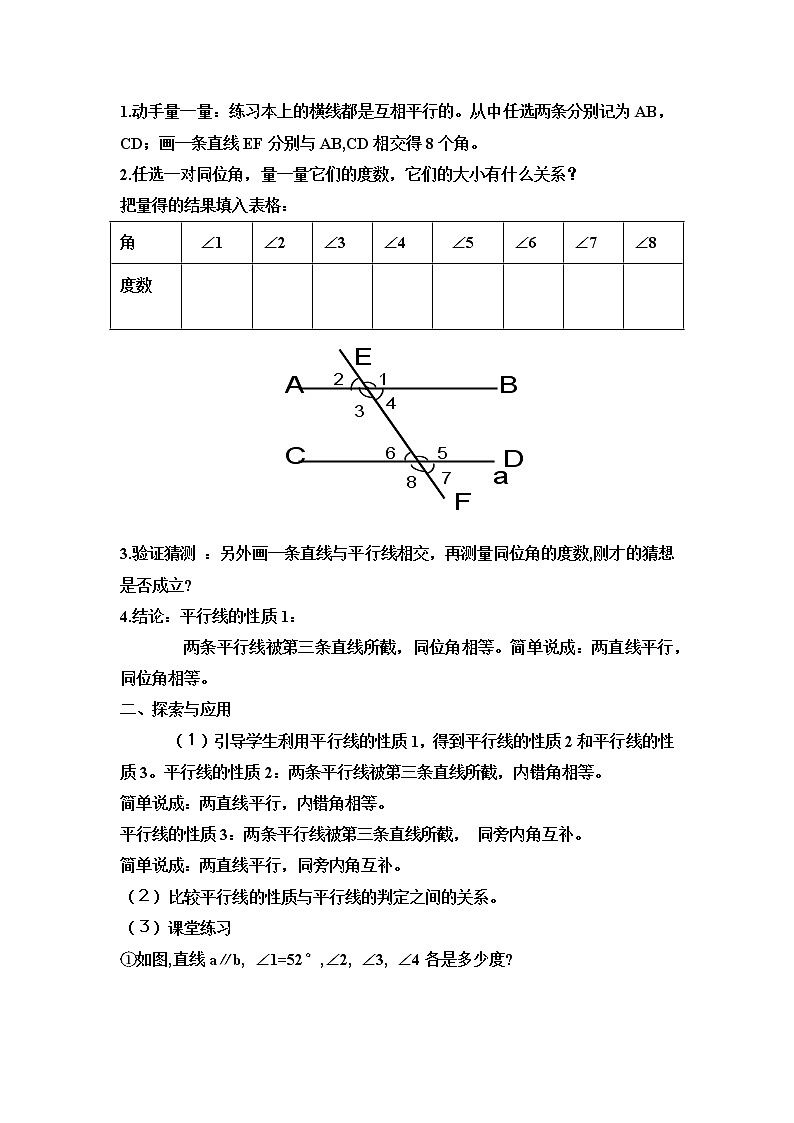
10．3平行线的性质学生知识状况分析    学生技能基础：在学习本课之前，学生有了初步的逻辑推理能力，特别是上一节课的学习，使学生对简单的证明步骤有了更为清楚的认识，这为今天的学习奠定了一个良好的基础．    活动经验基础：在以往的几何学习中，学生对动手操作、猜想、说理、讨论等活动形式比较熟悉，本节课主要采取学生分组交流、讨论等学习方式，学生已经具备必要的基础． 教学任务分析在以前的几何学习中，主要是针对几何概念、运算以及几何的初步证明（说理），在学生的头脑中还没有形成一个比较系统的几何证明体系，让学生从简单的几何证明（平行线的判定与性质）入手，逐步形成一个更为清晰的证明思路，为此，本课时的教学目标是：   1.认识平行线的三条性质。   2.能熟练运用这三条性质证明几何题。   3.进一步发展学生的合情推理能力，培养学生的逻辑思维能力。新课 标第 一 网教学过程本节课的设计分为四个环节：活动引入——探索与应用——反馈练习——反思与小结一、活动引入活动一：动手做一做：已知直线a及其外一点P，过点P画出直线 a 的平行线 b 。 （同学们动手操作）想一想：本例中，作图的理论依据是什么？追问：根据同位角相等，可以判定两条直线平行。反过来，如果两直线平行，同位角是否相等呢？ 活动二：1.动手量一量：练习本上的横线都是互相平行的。从中任选两条分别记为AB，CD；画一条直线EF分别与AB,CD相交得8个角。 2.任选一对同位角，量一量它们的度数，它们的大小有什么关系？ 把量得的结果填入表格：角  ∠1∠2∠3∠4 ∠5∠6∠7∠8度数          3.验证猜测 ：另外画一条直线与平行线相交，再测量同位角的度数,刚才的猜想是否成立?4.结论：平行线的性质1：        两条平行线被第三条直线所截，同位角相等。简单说成：两直线平行，同位角相等。二、探索与应用      （１）引导学生利用平行线的性质1，得到平行线的性质2和平行线的性质3。平行线的性质2：两条平行线被第三条直线所截，内错角相等。简单说成：两直线平行，内错角相等。平行线的性质3：两条平行线被第三条直线所截， 同旁内角互补。简单说成：两直线平行，同旁内角互补。（２）比较平行线的性质与平行线的判定之间的关系。（３）课堂练习①如图,直线a∥b, ∠1=52°,∠2, ∠3, ∠4各是多少度?解：∵  ∠1= 52°(已知)∴ ∠2=∠1 =52°(对顶角相等)∵  a∥b(已知)∴ ∠2+∠3=180°(两直线平行,同旁内角互补)∴  ∠3= 180°－ ∠2= 180°－52°=128°∴  ∠4=∠1=52°(两直线平行,同位角相等) ②如图，一条公路两次拐弯后，和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是136o，第二次拐的角∠C是多少度？为什么？答：∠C=136o  ∵ AB∥CD , ∠B=136°  ∴∠C=∠B=136°(两直线平行，内错角相等)三、反馈练习如图，已知点D，E，F分别在三角形ABC的边AB，AC，BC上，且DE∥BC，∠B=48°。 （1）试求∠ ADE 的度数； （2）如果∠DEF =48°，那么EF与AB平行吗？ 解：（1） ∵ DE∥BC, ∠B=48°（已知）∴∠ADE=∠B=48°(两直线平行，同位角相等) （2）由（1），得∠ADE=48°  又∵ ∠DEF =48°（已知）∴∠ADE=∠DEF（等量代换）∴DE∥BC  (两直线平行，同位角相等) 四、课堂小结谈一谈：本节课你有何收获？类比平行线的性质与平行线的判定  五、布置作业必做题：如图，D是AB上一点，E是AC上一点，∠ADE=60 ° ∠B=60 °∠AED=40°（１）DE和BC平行吗？为什么？（２） ∠C是多少度，为什么？   选做题：思考：如图所示是一大门的栏杆，AE为地面， BA⊥AE于点A，CD ∥AE,则∠ABC+ ∠BCD=          度。教学反思通过学生的动手操作，感知平行线的判定和性质，通过大胆的猜想，认真的验证，确定平行线的性质，学生增强了发现探究问题的能力。对于平行线的性质和判定的联系，少数学生还不是分辨很清楚，需要在以后的练习中巩固、明确。