高中数学北师大版 (2019)必修 第二册5.1 直线与平面垂直教课课件ppt

这是一份高中数学北师大版 (2019)必修 第二册5.1 直线与平面垂直教课课件ppt，共23页。PPT课件主要包含了教学目标，教学重难点，任何一条直线都垂直，两条相交直线垂直，点到平面的距离，有且仅有一条，垂线段，不与这个平面垂直，斜线和平面的交点，过垂足和斜足的直线等内容，欢迎下载使用。
1.了解空间中直线与平面的垂直关系；2.理解并掌握直线与平面垂直的性质定理；3.了解直线到平面的距离和直线与平面所成角的概念并会简单计算。
重点：1.直线与平面垂直的定义及性质定理； 2.直线与平面所成的角及其求法。难点：1.直线与平面垂直的性质定理的探究与应用； 2.直线与平面所成的角的求法。
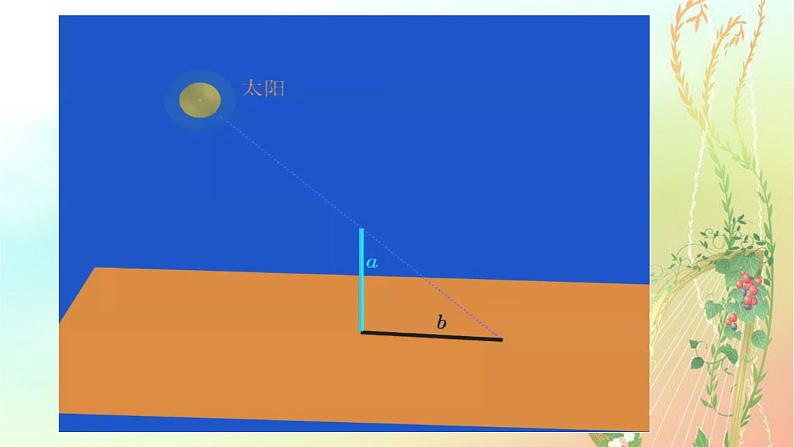
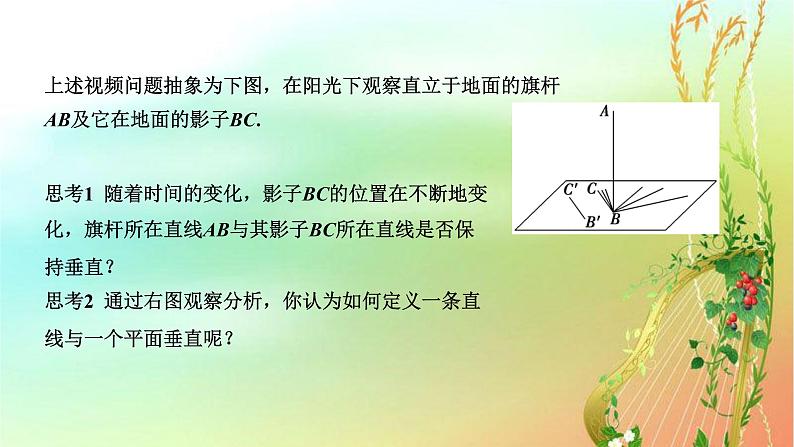
上述视频问题抽象为下图，在阳光下观察直立于地面的旗杆AB及它在地面的影子BC.
思考1 随着时间的变化，影子BC的位置在不断地变化，旗杆所在直线AB与其影子BC所在直线是否保持垂直？思考2 通过右图观察分析，你认为如何定义一条直线与一个平面垂直呢？
1．直线与平面垂直的定义：如果直线l与平面α内的 ，我们就说直线l与平面α互相垂直，记作 ，直线l叫做平面α的 ，平面α叫做直线l的垂面．直线与平面垂直时，它们唯一的公共点P叫做垂足．
2. 直线与平面垂直的画法：
文字语言：如果一条直线与一个平面内的 ，则该直线与此平面垂直．符号语言：l⊥a，l⊥b，a⊂α，b⊂α，a∩b＝P⇒l⊥α.图形语言：如图所示
注意：画直线l与平面α垂直时，通常把直线画成与表示平面的平行四边形的一边垂直。
过一点垂直于已知平面的直线 ．过一点作垂直于已知平面的直线，则该点与垂足间的线段，叫做这个点到该平面的 ， 的长度叫做这个点到该平面的距离．
4. 直线与平面垂直的判定定理文字语言：如果一条直线与一个平面内的 ，则该直线与此平面垂直．符号语言：图形语言：如图所示．
例4　如图，四棱锥S－ABCD的底面是矩形，SA⊥底面ABCD，E，F分别是SD，SC的中点．求证：
(1)BC⊥平面SAB；(2)EF⊥SD.
[证明]　(1)∵四棱锥S－ABCD的底面是矩形，∴AB⊥BC.∵SA⊥平面ABCD，BC⊂平面ABCD，∴SA⊥BC.又SA∩AB＝A，∴BC⊥平面SAB.(2)由(1)知BC⊥平面SAB.同理，CD⊥平面SAD.∵E，F分别是SD，SC的中点，∴EF∥CD，∴EF⊥平面SAD.
5.　直线与平面所成的角
思考：一条直线l和平面α相交但不垂直，这条直线叫平面的斜线．平面的斜线有很多条，它们和平面相交的程度不一样，如何刻画这种程度呢？
为了刻画直线和平面相交的程度，我们引入了直线和平面所成的角．
定义： ，但 ，这条直线叫做这个平面的斜线， 叫做斜足．过斜线上斜足以外的一点向平面引 ，与平面的交点为垂足， 叫做斜线在这个平面上的射影．平面的一条斜线和 ，叫做这条直线和这个平面所成的角，其范围是 ．
一条直线与一个平面相交
如图， 就是斜线AP与平面α所成的角．(2)当直线AP与平面垂直时，它们所成的角是 .(3)当直线与平面平行或在平面内时，它们所成的角是 .(4)直线与平面所成的角θ的范围： .
例5. 如图所示，若斜线段AB是它在平面α上的射影BO的2倍，则AB与平面α所成的角是(　　)A．60°B．45°C．30°D．120°
练习1．如图，在正方体ABCD­A1B1C1D1中，直线AB1与平面ABCD所成的角等于__________；AB1与平面ADD1A1所成的角等于__________；AB1与平面DCC1D1所成的角等于__________．
解：∠B1AB为AB1与平面ABCD所成的角即45°；∠B1AA1为AB1与平面ADD1A1所成的角，即45°；AB1与平面DCC1D1平行，即所成的角为0°.
练习2 如图所示，空间四边形ABCD中，AB＝CD，AB⊥CD，E、F分别为BC、AD的中点，求EF和AB所成的角．
练习3 如图所示，在正方体ABCD－A1B1C1D1中，E是棱DD1的中点．求直线BE与平面ABB1A1所成的角的正弦值．
变式 在上例中，若求直线BE与平面A1B1C1D1所成角的正弦值，又如何求解？