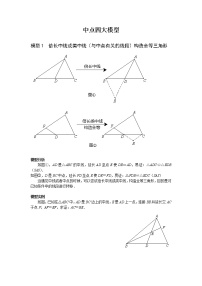
2022年中考数学几何模型提升专题01 中点弧模型

中考几何模型提升篇01——圆综合之中点弧模型

题型一 中点弧与相似

【模型解读】

点P是优弧AB上一动点，则

∠1＝∠2，∠PCB为公共角，子母型相似

【补充】⑥PE•PC＝PA•PB，

【例题1】

如图，四边形内接于，对角线、交于点，且，若，，则　　．

【巩固练习】

如图，是的直径，、为上位于异侧的两点，连接并延长至点，使得，连接交于点，连接、、．

（1）证明：；

（2）设交于点，若，是的中点，求的值．

题型二中点弧与旋转

【模型解读】点P是优弧AB上一动点，且点C是的中点

邻边相等+对角互补 旋转相似模型，一般用来求圆中三条线段之间的数量关系.



由于对角互补，即，显然共线，且，通过导角不难得出相似.

【例题2】

如图，已知是的弦，点是弧的中点，是弦上一动点，且不与、重合，的延长线交于点，连接、，过点作，垂足为，．

（1）求证：是的切线；

（2）若，，求的长；

（3）当点在弦上运动时，的值是否发生变化？如果变化，请写出其变化范围；如果不变，请求出其值．

【巩固练习1】

在的内接四边形中，，，，点为弧的中点，则的长是　　．

【巩固练习2】

已知内接于⊙O，∠BAC的平分线交⊙O于点D，连接DB，DC．

（1）如图①，当时，请直接写出线段AB，AC，AD之间满足的等量关系式：______________.

（2）如图②，当时，试探究线段AB，AC，AD之间满足的等量关系，并证明你的结论；

（3）如图③，若，，求的值．

题型三 中点弧+内心可得等腰

【模型讲解】外接圆+内心⇒得等腰

如图，圆O是△ABC外接圆圆心，I是三角形ABC的内心，延长AI交圆O于D，证DI＝DC＝BD



【简证】∠1＝∠4＋∠5,∠4＝∠3，∠2＝∠5∴∠1＝∠2＋∠3

【例题3】

如图1，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，过点C作∠BCD＝∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF．

（1）求证：ED＝EC；

（2）求证：AF是⊙O的切线；

（3）如图2，若点G是△ACD的内心，BC·BE＝25，求BG的长．

【巩固练习】

如图，点I是△ABC的内心，BI的延长线与△ABC的外接圆⊙O交于点D，与AC交于点E，延长CD、BA相交于点F，∠ADF的平分线交AF于点G．

（1）求证：DG∥CA；

（2）求证：AD＝ID；

（3）若DE＝4，BE＝5，求BI的长．

题型四 弧中点与垂径定理

【模型解读】

【例题4】

如图，为的直径，，为圆上的两点，，弦，相交于点．

（1）求证：；

（2）若，，求的半径．

【巩固练习】

如图，是的直径，为弦的中点，连接并延长交于点，连接交于点，延长至点，使得，连接．

（1）求证：是的切线；

（2）若的半径为5，，求的长．

题型五 弧中点与垂径模型（三等弧模型）

【例题5】

如图，△ABC内接于⊙O，AB是⊙O的直径，C是的中点，弦CE⊥AB于点H，连结AD，分别交CE、BC于点P、Q，连结BD。

(1)证CO∥BD

(2) AD＝CE

(3)证：P是线段AQ的中点

(4)证：CP·CE＝AH·AB＝CQ·CB

(5)tan∠DBC＝

(6)若AD＝8，BD＝6，求AH的值

(7) 若⊙O的半径为5，AQ＝，求弦CE的长.

【巩固练习】

如图，是的直径，点为的中点，为的弦，且，垂足为，连接交于点，连接，，．

（1）求证：；

（2）若，求的长．

中考几何模型提升篇01——圆综合之中点弧模型

题型一 中点弧与相似

【模型解读】

点P是优弧AB上一动点，则

∠1＝∠2，∠PCB为公共角，子母型相似

【补充】⑥PE•PC＝PA•PB，注意：⑥不能反推出前五项

【例题1】

如图，四边形内接于，对角线、交于点，且，若，，则　　．

易知，则，

【巩固练习】

如图，是的直径，、为上位于异侧的两点，连接并延长至点，使得，连接交于点，连接、、．

（1）证明：；

（2）设交于点，若，是的中点，求的值．

【解答】证明：（1）是的直径，

，即，

，

垂直平分，

，

，

又，

；

（2）连接，

，

是的中点，是的直径，

，

，

，

是的中点，

，

，

，

即．

题型二中点弧与旋转

【模型解读】点P是优弧AB上一动点，且点C是的中点

邻边相等+对角互补 旋转相似模型，一般用来求圆中三条线段之间的数量关系.



由于对角互补，即，显然共线，且，通过导角不难得出相似.

【例题2】

如图，已知是的弦，点是弧的中点，是弦上一动点，且不与、重合，的延长线交于点，连接、，过点作，垂足为，．

（1）求证：是的切线；

（2）若，，求的长；

（3）当点在弦上运动时，的值是否发生变化？如果变化，请写出其变化范围；如果不变，请求出其值．

（1）证切线一般先导角

（2）通过弧中点所对应的相似模型可以口算

（3）可以考虑通过旋转构造出分母的所对应的线段，再通过相似或三角函数得出比值.

当然，（3）还有很多方法，比如利用角平分线作垂线

求数量关系的话，截长补短也是常见方法，得到的图形与之前旋转法类似，不过辅助线做法不一样

除此之外，构造旋转相似也是一种处理方式，这里就不细讲了可以结合图形自行体会





（1）证明：如图，连接，，，交于，

，，

是等边三角形，

，

点是弧的中点，

，

，

，

，

，

，

，

，

，

，

是的切线；

（2）解：，

，

，

，

，

，

，

；

（3）结论：，的值不变．

理由：如图，连接，，交于，作交的延长线于，

，

，

由（1）得，，

，

，

，

，

，

，

，，

，

，，

，

，

，

，

的值不变．

【巩固练习1】

在的内接四边形中，，，，点为弧的中点，则的长是　　．

解法一、、、、四点共圆，，

，

，平分，

，

如图，将绕点逆时针旋转得，

则，，，

，

、、三点共线，

过作于，

，

，

在中，；

解法二、如图，过作于，于，

则，

点为弧的中点，

，

，，

，，

，

、、、四点共圆，

，

在和中

，

，

，

在和中，

，

，

，

设，

，，

，

，

解得：，

即，

，

故答案为．

【巩固练习2】

已知内接于⊙O，∠BAC的平分线交⊙O于点D，连接DB，DC．

（1）如图①，当时，请直接写出线段AB，AC，AD之间满足的等量关系式：______________.

（2）如图②，当时，试探究线段AB，AC，AD之间满足的等量关系，并证明你的结论；

（3）如图③，若，，求的值．

（1）

（2）

（3）

题型三 中点弧+内心可得等腰

【模型讲解】外接圆+内心⇒得等腰

如图，圆O是△ABC外接圆圆心，I是三角形ABC的内心，延长AI交圆O于D，证DI＝DC＝BD



【简证】∠1＝∠4＋∠5,∠4＝∠3，∠2＝∠5∴∠1＝∠2＋∠3

【例题3】

如图1，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，过点C作∠BCD＝∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF．

（1）求证：ED＝EC；

（2）求证：AF是⊙O的切线；

（3）如图2，若点G是△ACD的内心，BC·BE＝25，求BG的长．

（1）由AB＝AC知∠ABC＝∠ACB，结合∠ACB＝∠BCD，∠ABC＝∠ADC得∠BCD＝∠ADC，从而得证；
（2）连接OA，由∠CAF＝∠CFA知∠ACD＝∠CAF＋∠CFA＝2∠CAF，结合∠ACB＝∠BCD得∠ACD＝2∠ACB，∠CAF＝∠ACB，据此可知AF∥BC，从而得OA⊥AF，从而得证；
（3）证△ABE∽△CBA得AB2＝BC•BE，据此知AB＝5，连接AG，得∠BAG＝∠BAD＋∠DAG，∠BGA＝∠GAC＋∠ACB，由点G为内心知∠DAG＝∠GAC，结合∠BAD＋∠DAG＝∠GAC＋∠ACB得∠BAG＝∠BGA，从而得出BG＝AB＝5．

解：（1）∵AB＝AC，
∴∠ABC＝∠ACB，
又∵∠ACB＝∠BCD，∠ABC＝∠ADC，
∴∠BCD＝∠ADC，
∴ED＝EC；
（2）如图，连接OA，

∵AB＝AC，
∴，
∴OA⊥BC，
∵CA＝CF，
∴∠CAF＝∠CFA，
∴∠ACD＝∠CAF＋∠CFA＝2∠CAF，
∵∠ACB＝∠BCD，
∴∠ACD＝2∠ACB，
∴∠CAF＝∠ACB，
∴AF∥BC，
∴OA⊥AF，
∴AF为⊙O的切线；
（3）∵∠ABE＝∠CBA，∠BAD＝∠BCD＝∠ACB，
∴△ABE∽△CBA，
∴，
∴AB2＝BC•BE，
∵BC•BE＝25，
∴AB＝5，
如图，连接AG，

∴∠BAG＝∠BAD＋∠DAG，∠BGA＝∠GAC＋∠ACB，
∵点G为内心，
∴∠DAG＝∠GAC，
又∵∠BAD＋∠DAG＝∠GAC＋∠ACB，
∴∠BAG＝∠BGA，
∴BG＝AB＝5．

【巩固练习】

如图，点I是△ABC的内心，BI的延长线与△ABC的外接圆⊙O交于点D，与AC交于点E，延长CD、BA相交于点F，∠ADF的平分线交AF于点G．

（1）求证：DG∥CA；

（2）求证：AD＝ID；

（3）若DE＝4，BE＝5，求BI的长．

（1）根据三角形内心的性质得∠2＝∠7，再利用圆内接四边形的性质得∠ADF＝∠ABC，则∠1＝∠2，从而得到∠1＝∠3，则可判断DG∥AC；

（2）根据三角形内心的性质得∠5＝∠6，然后证明∠4＝∠DAI得到DA＝DI；

（3）证明△DAE∽△DBA，利用相似比得到AD＝6，则DI＝6，然后计算BD－DI即可．

（1）证明：∵点I是△ABC的内心，

∴∠2＝∠7，

∵DG平分∠ADF，

∴∠1＝

∵∠ADF＝∠ABC，

∴∠1＝∠2，

∵∠3＝∠2，

∴∠1＝∠3，

∴DG∥AC；

（2）证明：∵点I是△ABC的内心，

∴∠5＝∠6，

∵∠4＝∠7＋∠5＝∠3＋∠6，

即∠4＝∠DAI，

∴DA＝DI；

（3）解：∵∠3＝∠7，∠ADE＝∠BDA，

∴△DAE∽△DBA，

∴AD：DB＝DE：DA，即AD：9＝4：AD，

∴AD＝6，

∴DI＝6，

∴BI＝BD－DI＝9－6＝3．

题型四 弧中点与垂径定理

【模型解读】

【例题4】

如图，为的直径，，为圆上的两点，，弦，相交于点．

（1）求证：；

（2）若，，求的半径．

（1）证明：，

，

，

，

，

；

（2）连接，

，，

，

，

，

，

，

，即，

解得，，

是直径，

，

，

的半径为．

【巩固练习】

如图，是的直径，为弦的中点，连接并延长交于点，连接交于点，延长至点，使得，连接．

（1）求证：是的切线；

（2）若的半径为5，，求的长．

解：（1）为弦的中点，是半径，

，

即，

，

又，

，

又，

，

，

，

即，

是半径，

是的切线；

（2）为弦的中点，

，

是半径，

，

在中，

，

又，，

，

，

即，

解得，，

．

题型五 弧中点与垂径模型（三等弧模型）

【例题5】

如图，△ABC内接于⊙O，AB是⊙O的直径，C是的中点，弦CE⊥AB于点H，连结AD，分别交CE、BC于点P、Q，连结BD。

(1)证CO∥BD

(2) AD＝CE

(3)证：P是线段AQ的中点

(4)证：CP·CE＝AH·AB＝CQ·CB

(5)tan∠DBC＝

(6)若AD＝8，BD＝6，求AH的值

(7) 若⊙O的半径为5，AQ＝，求弦CE的长.

（1）

（2）

(3)先利用弧相等导角证AP＝CP，再通过Rt△ACQ中的互余关系，得到PQ＝CP，

∴AP＝PQ＝CP

（4）CP＝AP，CE＝AD⇒CP•CE＝AP•AD，△APH∼△ABD⇒AP•AD＝AH•AB

（5）

（6）法一

（6）法二

（7）找到对应相似三角形是关键

【巩固练习】

如图，是的直径，点为的中点，为的弦，且，垂足为，连接交于点，连接，，．

（1）求证：；

（2）若，求的长．

证明：（1）是的中点，

，

是的直径，且，

，

，

，

在和中，

，

；

（2）解法一：如图，连接，设的半径为，

中，，即，

中，，即，

，

，

，

，

即，

解得：（舍或3，

，

；

解法二：如图，过作于，连接、，

，

，

，

，

，

，

，

，，

，

，

，

，

是的直径，

，

，

，

，

，

，

．

解法三：如图，连接，交于，

是的中点，

，

，

，

，

，，，

，

，

，

．