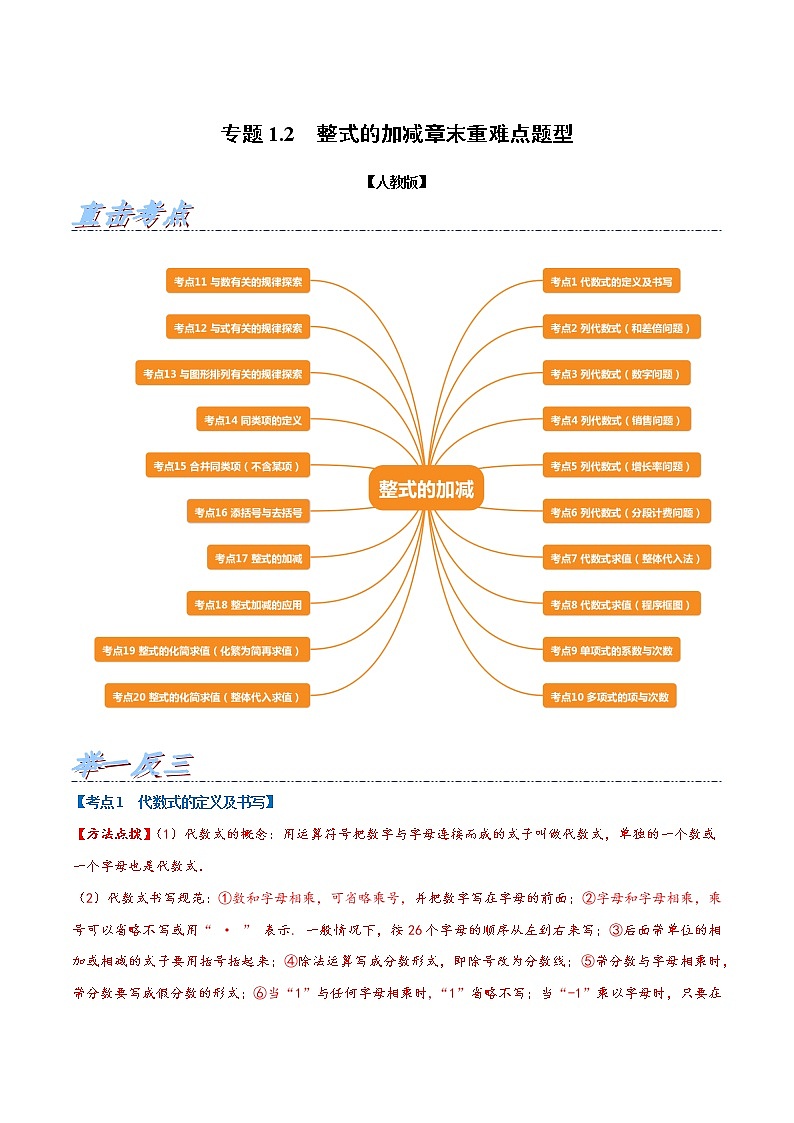


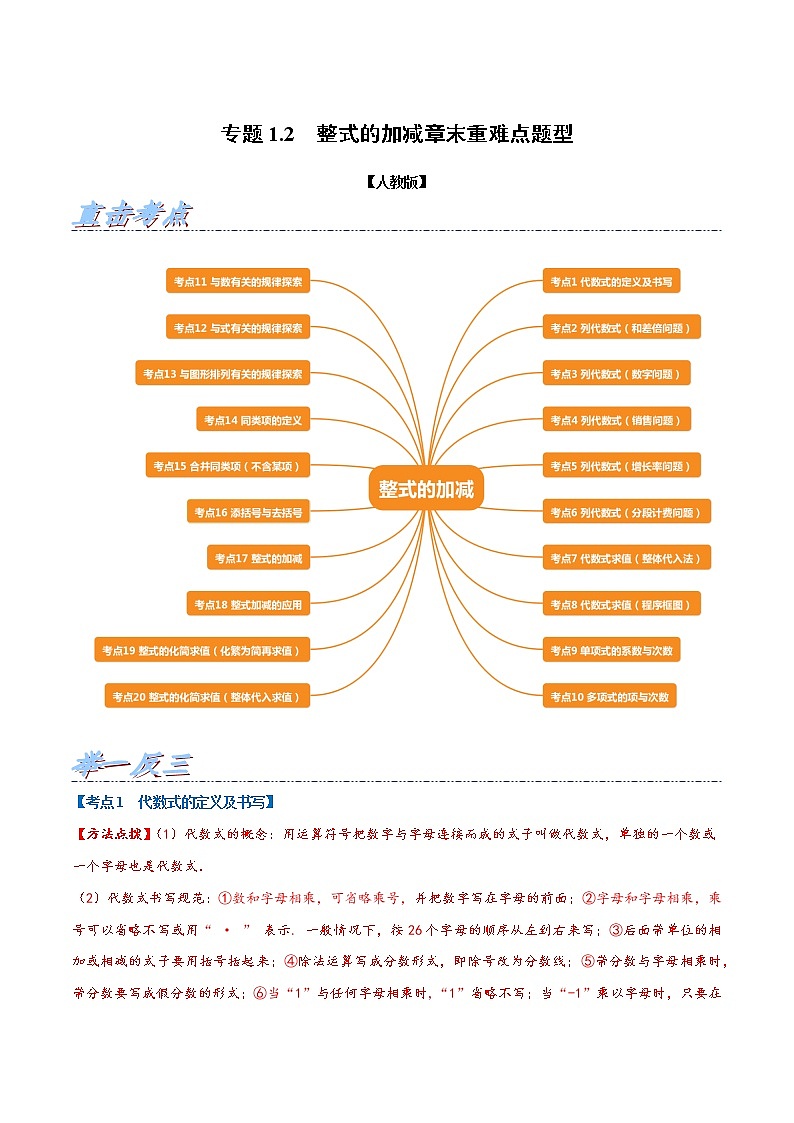


专题1.2 整式的加减章末重难点题型-2021-2022学年七年级数学上册举一反三系列(人教版)
展开专题1.2 整式的加减章末重难点题型
【人教版】
【考点1 代数式的定义及书写】
【方法点拨】(1)代数式的概念:用运算符号把数字与字母连接而成的式子叫做代数式,单独的一个数或
一个字母也是代数式.
(2) 代数式书写规范:①数和字母相乘,可省略乘号,并把数字写在字母的前面;②字母和字母相乘,乘
号可以省略不写或用“ · ” 表示. 一般情况下,按26个字母的顺序从左到右来写;③后面带单位的相加或相减的式子要用括号括起来;④除法运算写成分数形式,即除号改为分数线;⑤带分数与字母相乘时,带分数要写成假分数的形式;⑥当“1”与任何字母相乘时,“1”省略不写;当“-1”乘以字母时,只要在
那个字母前加上“-”号.
【例1】(1)(2019秋•皇姑区校级期中)在下列各式中(1)3a,(2)4+8=12,(3)2a﹣5b>0,(4)0,(5)s=πr2,(6)a2﹣b2,(7)1+2,(8)x+2y,其中代数式的个数是( )
A.3个 B.4个 C.5个 D.6个
(2)(2019秋•茂名期中)下列各式:①114x;②2•3;③20%x;④a﹣b÷c;⑤m-n3;⑥x﹣5千克:其中符合代数式书写要求的有( )
A.5个 B.4个 C.3个 D.2个
【变式1-1】(2019秋•杨浦区校级月考)在以下各式中属于代数式的是( )
①S=12ah②a+b=b+a③a④1a⑤0 ⑥a+b⑦a+bab
A.①②③④⑤⑥⑦ B.②③④⑤⑥ C.③④⑤⑥⑦ D.①②
【变式1-2】(2019秋•桥西区校级月考)在式子0.5xy﹣2,3÷a,12(a+b),a•5,﹣314abc中,符合代数式书写要求的有( )
A.1个 B.2个 C.3个 D.4个
【变式1-3】(2019秋•南昌期末)进入初中后学习数学,对于代数式书写规范,教材中指出:“在含有字母的式子中如果出现乘号“×”,通常将乘号写作“•”或者省略不写”.其实还有一些书写规范,比如,在代数式中如果出现除号“÷”,通常用分数线“﹣”来取代;数字与字母相乘时,一般数字写在前面,根据以上书写要求,将代数式(ac×4﹣b2)÷4简写为 .
【考点2 列代数式(和差倍问题)】
【方法点拨】解决此类问题是要理解题意,将字母看作数字表示相应的量,列出代数式,注意代数式
的书写规范.
【例2】(2019秋•宿豫区期中)学校举行国庆画展,七(1)班交m件作品,七(2)班交的作品比七(1)班的2倍少6件,则七(2)班交的作品是 件.
【变式2-1】(2019秋•临沭县期中)某校报数学兴趣小组的有m人,报书法兴趣小组的人数比数学兴趣小组的人数的一半多3人,那么报书法兴趣小组的有 人.
【变式2-3】(2019秋•孝义市期中)某学校七年级有m人,八年级人数比七年级人数的23多10人,九年级人数比八年级人数的2倍少50人,用含m的式子表示七八九三个年级的总人数为( )
A.3m B.113m﹣40 C.3m﹣40 D.3m﹣20
【变式2-3】(2019秋•九江期中)我校甲、乙、丙三位同学给希望工程捐款,已知甲同学捐款x元,乙同学的捐款金额比甲同学捐款金额的3倍少8元,丙同学的捐款金额是甲、乙两同学捐款总金额的34,用含x的代数式表示甲,乙、丙三位同学的捐款总金额.
【考点3 列代数式(数字问题)】
【方法点拨】解决此类问题是要理解题意,将字母看作数字表示相应的量,列出代数式,注意代数式
的书写规范.
【例3】(2020春•香坊区校级期中)一个两位数,十位上的数字为a,个位上的数字比十位上的数字少2,则这个两位数为( )
A.11a﹣20 B.11a+20 C.11a﹣2 D.11a+2
【变式3-1】(2019春•新泰市期中)设a是一个三位数,b是一个两位数,如果将这两个数顺次排成一个五位数(a在左,b在右),则这个五位数可以表示为 .
【变式3-2】(2019秋•温岭市期中)一个三位数为x,一个两位数为y,把这个三位数放在两位数的左边得到一个五位数M,把这个两位数放在三位数的左边又可以得到一个五位数N,则M﹣N= (结果用含x,y的式子表示).
【变式3-3】(2019秋•临高县期中)用式子表示十位上的数是x,个位上的数是y的两位数,再把这个两位数的十位上的数与个位上的数交换位置.求后来所得的数与原来的数的差是多少?
【考点4 列代数式(销售问题)】
【方法点拨】解决此类问题是要理解题意,将字母看作数字表示相应的量,列出代数式,注意代数式
的书写规范.
【例4】(2019秋•洪山区期中)一件羽毛球拍先按成本价提高50%标价,再将标价打8折出售,若这件羽毛球拍的成本价是x元,那么售价可表示为 .
【变式4-1】(2019春•南岗区校级期中)某商店有一种商品每件成本a元,按成本价增加20%定为售价,售出80件后,由于存积压降价,打八五折出售,又售出120件.
(1)求该商品减价后每件的售价为多少元?
(2)售完200件这种商品共盈利多少元?
【变式4-2】(2019秋•行唐县期中)小明经销一种服装,进货价为每件a元,经测算先将进货价提高200%进行标价,元旦前夕又按标价的4折销售,这件服装的实际价格( )
A.比进货价便宜了0.52a元
B.比进货价高了0.2a元
C.比进货价高了0.8a元
D.与进货价相同
【变式4-3】(2019秋•海曙区期中)张师傅下岗后做起了小生意,第一次进货时,他以每件a元的价格购进了20件甲种小商品,以每件b元的价格购进了30件乙种小商品(a>b).根据市场行情,他将这两种小商品都以a+b2元的价格出售.在这次买卖中,张师傅的盈亏状况为( )
A.赚了(25a+25b)元 B.亏了(20a+30b)元
C.赚了(5a﹣5b)元 D.亏了(5a﹣5b)元
【考点5 列代数式(增长率问题)】
【方法点拨】解决此类问题是要理解题意,将字母看作数字表示相应的量,列出代数式,注意代数式
的书写规范.
【例5】(2019秋•牡丹江期中)某校去年初一招收新生a人,今年比去年增加x%,今年该校初一学生人数用式子表示为( )
A.(a+x%)人 B.ax%人
C.a(1+x)100人 D.a(1+x%)人
【变式5-1】(2019秋•海淀区校级期中)某校初一年级计划初中三年每年参加植树活动,2019年已经植树a亩,如果以后每年比上一年植树面积增长20%,那么2021应植树的面积为( )
A.a•(1+20%) B.a•(1+2×20%)
C.a•(1+20%)2 D.2a•(1+20%)
【变式5-2】(2019秋•开福区校级期中)某企业今年1月份产值为x万元,2月份的产值比1月份减少了10%,则1月份和2月份的产值和是( )
A.x+(1﹣10%)x万元 B.x+(1+10%)x万元
C.(1﹣10%)x万元 D.(1+10%)x万元
【变式5-3】(2019秋•揭阳期末)裕丰商店一月份的利润为50万元,二、三月份的利润平均增长率为m,则下列各式中,能正确表示这个商店第一季度的总利润的是( )
A.50(1+m)万元
B.50(1+m)2万元
C.[50+50(1+m)]万元
D.[50+50(1+m)+50(1+m)2]万元
【考点6 列代数式(分段计费问题)】
【方法点拨】解决此类问题是要理解题意,将字母看作数字表示相应的量,列出代数式,注意代数式
的书写规范.
【例6】(2019秋•东西湖区期中)东西湖区域出租汽车行驶2千米以内(包括2千米)的车费是10元,以后每行驶1千米,再加0.7元.如果某人坐出租汽车行驶了m千米(m是整数,且m≥2),则车费是( )
A.(10﹣0.7m)元 B.(11.4+0.7m)元
C.(8.6+0.7m)元 D.(10+0.7m)元
【变式6-1】(2019秋•玄武区期中)为响应国家节能减排的号召,鼓励人们节约用电,保护能源,某市实施用电“阶梯价格”收费制度.收费标准如表:
居民每月用电量
单价(元/度)
不超过50度的部分
0.5
超过50度但不超过200度的部分
0.6
超过200度的部分
0.8
已知小刚家上半年的用电情况如下表(以200度为标准,超出200度记为正、低于200度记为负):
一月份
二月份
三月份
四月份
五月份
六月份
﹣50
+30
﹣26
﹣45
+36
+25
根据上述数据,解答下列问题:
(1)小刚家用电量最多的是 月份,实际用电量为 度;
(2)小刚家一月份应交纳电费 元;
(3)若小刚家七月份用电量为x度,求小刚家七月份应交纳的电费(用含x的代数式表示).
【变式6-2】(2019秋•金乡县期中)为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米)
价目表
每月用水量
单价
不超过6m3的部分
2元/m3
超出6m3不超出10m3的部分
4元/m3
超出10m3的部分
8元/m3
请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5m3,则应交水费 元;3月份用水8m3,则应收水费 元;
(2)若该户居民4月份用水am3(其中a>10m3),则应交水费多少元(用含a的代数式表示,并化简)?
(3)若该户居民5、6两个月共用水14m3(6月份用水量超过了5月份),设5月份用水xm3,直接写出该户居民5、6两个月共交水费多少元(用含x的代数式表示).
【变式6-3】(2019秋•洪山区期中)滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.45元/分钟
0.4元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算:
时长费按行车的实际时间计算远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元.
(1)若小东乘坐滴滴快车,行车里程为20公里,行车时间为30分钟,则需付车费 元;
(2)若小明乘坐滴滴快车,行车里程为a公里,行车时间为b分钟,则小明应付车费多少元;(用含a、b的代数式表示,并化简)
(3)小王与小张各自乘坐滴滴快车,行车里程分别为9.5公里与14.5公里,受路况情况影响,小王反而比小张乘车多用24分钟,请问谁所付车费多?
【考点7 代数式求值(整体代入法)】
【例7】(2019秋•福田区期中)已知代数式x﹣2y的值是3,则代数式4y+1﹣2x的值是( )
A.﹣5 B.﹣3 C.﹣1 D.0
【变式7-1】(2019秋•郾城区期中)当x=2时,代数式px3+qx+1的值为﹣2019,求当x=﹣2时,代数式的px3+qx+1值是( )
A.2018 B.2019 C.2020 D.2021
【变式7-2】(2019春•海阳市期中)已知1﹣a2+2a=0,则14a2-12a+54的值为( )
A.32 B.14 C.1 D.5
【变式7-3】(2019秋•甘井子区期末)(1)【探究】若a2+2a=1,则代数式2a2+4a+4=2( )+4=2×( )+4= .
【类比】若x2﹣3x=2,则x2﹣3x﹣5的值为 .
(2)【应用】当x=1时,代数式px3+qx+1的值是5,求当x=﹣1时,px3+qx+1的值;
(3)【推广】当x=2020时,代数式ax5+bx3+cx﹣5的值为m,当x=﹣2020时,ax5+bx3+cx﹣5的值
为 (含m的式子表示)
【考点8 代数式求值(程序框图)】
【例8】(2019秋•九龙坡区校级期中)根据以下程序,当输入x=﹣2时,输出结果为( )
A.﹣5 B.﹣16 C.5 D.16
【变式8-1】(2019秋•巴南区期中)根据如图所示的计算程序,若输入x=﹣1,则输出结果为( )
A.4 B.2 C.1 D.﹣1
【变式8-2】(2019春•沙坪坝区校级期中)按如图所示的运算程序,能使运算输出的结果为6的是( )
A.x=5,y=﹣1 B.x=2,y=2 C.x=2,y=﹣1 D.x=﹣2,y=3
【变式8-3】(2019秋•南岸区期中)如图是一个运算程序,能使输出结果为﹣1的是( )
A.1,2 B.﹣1,0 C.﹣1,2 D.0,﹣1
【考点9 单项式的系数与次数】
【方法点拨】解题关键:①单项式中的数字因数称为这个单项式的系数;②一个单项式中,所有字
母的指数的和叫做这个单项式的次数
【例9】(2019秋•海淀区校级期中)4πx2y4z9的系数是 ,次数是 .
【变式9-1】(2019秋•淅川县期中)单项式﹣3πxa+1y2与-102x2y39的次数相同,则a的值为 .
【变式9-2】(2019秋•永吉县期末)若单项式﹣x3yn+5的系数是m,次数是9,则m+n的值为 .
【变式9-3】(2019秋•鄂城区期中)已知(m﹣3)x3y|m|+1是关于x,y的七次单项式,求m2﹣2m+2= .
【考点10 多项式的项与次数】
【方法点拨】解题关键是熟悉几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数.
【例10】(2019秋•北碚区校级期中)关于多项式5x4y﹣3x2y+4xy﹣2,下列说法正确的是( )
A.三次项系数为3
B.常数项是﹣2
C.多项式的项是5x4y,3x2y,4xy,﹣2
D.这个多项式是四次四项式
【变式10-1】(2019秋•禹州市期中)多项式 是一个关于x的三次四项式,它的次数最高项的系数是﹣5,二次项的系数是34,一次项的系数是﹣2,常数项是4.
【变式10-2】(2019秋•高安市期中)已知关于x的整式(|k|﹣3)x3+(k﹣3)x2﹣k.
(1)若此整式是单项式,求k的值;
(2)若此整式是二次多项式,求k的值;
(3)若此整式是二项式,求k的值.
【变式10-3】(2019秋•吉林期中)已知关于x、y的多项式-35x2ym+1+12x2y2-3y2+8是八次四项式,单项式5xny6﹣m的次数与该多项式的次数相同,求m、n的值.
【分析】先根据多项式的次数计算出m的值,再根据单项式的次数计算出n的值即可.
【考点11 与数有关的规律探索】
【例11】(2019秋•灌云县期中)根据图中数字的规律,则x+y的值是( )
A.729 B.550 C.593 D.738
【变式11-1】(2019秋•安庆期中)将全体正奇数排成一个三角形数阵如下,按照以上排列的规律,第19行第11个数是( )
A.363 B.361 C.359 D.357
【变式11-2】(2020春•竹溪县期末)将全体自然数按下面的方式进行排列,按照这样的排列规律,2020应位于( )
A.位 B.位 C.位 D.位
【变式11-3】(2020•昆明模拟)按规律排列的一列数:-12,25,-38,411,-514,…,则第2020个数是 .
【考点12 与式有关的规律探索】
【例12】(2019秋•武安市期中)从2开始,连续n个偶数相加的合计为S,它们和的情况如下表:
(1)若n=8时,则S的值为 .
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n= .
加数的个数n
S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
(3)根据上题的规律计算2+4+6+8+10+…+2018+2020的值.
【变式12-1】(2019秋•自贡期中)已知a是不为1的有理数,我们把11-a称为a的差倒数,如2的差倒数是11-2=-1.现已知a1=12,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
(1)求a2,a3,a4的值.
(2)根据(1)的计算结果,请猜想并写出a2018•a2019•a2020的值.
(3)计算:a1+a2+a3+…+a2018+a2019.
【变式12-2】(2019秋•方城县期中)小学的时候我们已经学过分数的加减法法则:“同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,转化为同分母分数,再加减.”如:12-13=32×3-22×3=3-22×3=12×3=16,反之,这个式子仍然成立,即:16=12×3=3-22×3=32×3-22×3=12-13
(1)问题发现
观察下列等式:
①11×2=2-11×2=21×2-11×2=1-12,
②12×3=3-22×3=32×3-22×3=12-13,
③13×4=4-33×4=43×4-32×3=13-14,…,
猜想并写出第n个式子的结果:1n(n+1)= .(直接写出结果,不说明理由)
(2)类比探究
将(1)中的的三个等式左右两边分别相加得:11×2+12×3+13×4=1-12+12-13+13-14=1-14=34,类比该问题的做法,请直接写出下列各式的结果:
①11×2+12×3+13×4+⋯+12019×2020= ;
②11×2+12×3+13×4+⋯+1n(n+1)= ;
(3)拓展延伸
计算:11×3+13×5+15×7+⋯+199×101.
【变式12-3】(2020春•淮阴区期中)阅读材料:
求1+2+22+23+24+…+22020的值.
解:设S=1+2+22+23+24+…+22020,将等式两边同时乘以2得,
2S=2+22+23+24+25+…+22021.
将下式减去上式,得2S﹣S=22021﹣1,即S=22021﹣1.
即1+2+22+23+24+…+22020=22021﹣1
仿照此法计算:
(1)1+3+32+33+…+320;
(2)1+12+122+123+⋯+12100.
【考点13 与图形排列有关的规律探索】
【例13】(2020春•鄂州期中)如图图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑥个图形中菱形的个数为( )
A.42 B.43 C.56 D.57
【变式13-1】(2019秋•江阴市期中)观察如图所示一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第10个图中共有点的个数是( )
A.109个 B.136个 C.166个 D.199个
【变式13-2】(2019秋•青岛期中)将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去…
(1)根据图中的规律补全下表:
图形标号
1
2
3
4
5
6
…
n
正方形个数
1
4
7
10
…
(2)求第几幅图形中有2020个正方形?
【变式13-3】(2019秋•延平区期中)某餐厅中1张餐桌可坐6人,有以下两种摆放方式:
(1)对于方式一:4张桌子拼在一起可坐 人;对于方式二,n张桌子拼在一起可坐 人;
(2)该餐厅有40张这样的长方形桌子,若按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改成每8张拼成一张大桌子,按方式二的拼法,则40张桌子共可坐多少人?
(4)一天中午,该餐厅来了98位顾客共同就餐,要求用满座位,但餐厅中只有25张这样的长方形桌子可用,若你是这家餐厅的经理,你打算选择哪种方式来摆餐桌呢(不考虑场地等因素)?
【考点14 同类项的定义】
【方法点拨】解题关键是掌握同类项的定义:所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
【例14】(2019秋•西城区校级期中)下列各组式子中是同类项的是( )
A.2x3与3x2 B.12ax 与8bx C.x4与a4 D.23与32
【变式14-1】(2020春•淇县期中)﹣2a2m+3b5与3a5bm﹣2n是同类项,则(m+n)2020的值是( )
A.1 B.﹣1 C.2 D.4
【变式14-2】(2019秋•路南区期中)如果单项式﹣3xay5与x3ya+b的和是单项式,那么a与b的值分别是( )
A.a=3,b=5 B.a=5,b=3 C.a=3,b=2 D.a=2,b=3
【变式14-3】(2019秋•牡丹江期中)如果2x3y|n|与-13xm+1y的和是单项式,则m+n的值是( )
A.1 B.﹣1 C.±1 D.3或1
【考点15 合并同类项(不含某项)】
【方法点拨】解题关键是首先进行合并同类项,不含某项,则该项的系数为0,从而求得结果.
【例15】(2019秋•九龙坡区期中)若代数式x2﹣2kxy+y2﹣6xy+9不含xy项,则k的值为( )
A.3 B.-12 C.0 D.﹣3
【变式15-1】(2019秋•西城区校级期中)若关于x的多项式x4﹣ax3+x3﹣5x2﹣bx﹣3x﹣1不存在含x的一次项和三次项,则a+b= .
【变式15-2】(2019秋•海淀区校级期中)若关于x,y的多项式my3+nx2y+2y3﹣x2y+y中不含三次项,则2m+3n= .
【变式15-3】(2019秋•东台市期中)已知代数式2x2+ax﹣y+6﹣2bx2+3x﹣5y﹣1的值与字母x的取值无关,求ab的值.
【考点16 添括号与去括号】
【方法点拨】解题关键是掌握(1)括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“﹣”,去括号后,括号里的各项都改变符号.运用这一法则去括号;
(2)添括号后,括号前是“+”,括号里的各项都不改变符号;添括号后,括号前是“﹣”,括号里的各项都改变符号.运用这一法则添括号.
【例16】(2019秋•大东区期末)下列去括号或添括号的变形中,正确的是( )
A.2a﹣(5b﹣c)=2a﹣5b﹣c B.3a+5(2b﹣1)=3a+10b﹣1
C.4a+3b﹣2c=4a+(3b﹣2c) D.m﹣n+a﹣2b=m﹣(n+a﹣2b)
【变式16-1】(2019秋•邓州市期末)在等式1﹣a2+2ab﹣b2=1﹣( )中,括号里应填( )
A.a2﹣2ab+b2 B.a2﹣2ab﹣b2 C.﹣a2﹣2ab+b2 D.﹣a2+2ab﹣b2
【变式16-2】(2019秋•金台区期末)已知a﹣b=﹣3,c+d=2,则(b+c)﹣(a﹣d)的值为( )
A.1 B.5 C.﹣5 D.﹣1
【变式16-3】(2019秋•杨浦区校级月考)不改变式子的值,把括号前的符号变成相反的符号x﹣y﹣(﹣y3+x2﹣1)= .
【考点17 整式的加减】
【例17】(2019秋•雅安期末)一个多项式加上12y+7x+z2等于5y+3x﹣15z2,则这个多项式是( )
A.﹣7y﹣4x﹣16z2 B.7y+4x+16z2
C.17y+10x﹣14z2 D.7y+4x﹣16z2
【变式17-1】(2019秋•东阿县期末)设M=x2﹣8x﹣4,N=2x2﹣8x﹣3,那么M与N的大小关系是( )
A.M>N B.M=N C.M<N D.无法确定
【变式17-2】(2019秋•潍坊期末)一个多项式M减去多项式﹣2x2+5x﹣3,小马虎同学却误解为先加上这个多项式,结果得x2+3x+7,则多项式M是( )
A.3x2﹣2x+10 B.﹣x2+8x+4 C.3x2﹣x+10 D.x2﹣8x﹣4
【变式17-3】(2019秋•石城县期末)在整式的加减练习课中,已知A=3a2b﹣2ab2+abc,小江同学错将“2A﹣B”看成“2A+B”,算得错误结果是4a2b﹣3ab2+4abc,已知.请你解决以下问题:
(1)求出整式B;
(2)求正确计算结果;
(3)若增加条件:a、b满足|a﹣4|+(b+1)2=0,你能求出(2)中代数式的值吗?如果能,请求出最后的值;如果不能,请说明理由.
【考点18 整式加减的应用】
【例18】(2019秋•香洲区期末)把一个大正方形和四个相同的小正方形按图①、②两种方式摆放,则大正方形的周长与小正方形的周长的差是( )
A.a+2b B.a+b C.3a+b D.a+3b
【变式18-1】(2019秋•鄞州区期末)如图,大长方形被分割成4个标号分别为(1)(2)(3)(4)的小正方形和5个小长方形,其中标号为(5)的小长方形的周长为a,则大长方形的周长为( )
A.3a B.4a C.5a D.6a
【变式18-2】(2020•余姚市模拟)在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图2中阴影部分的周长与图1中阴影部分的周长的差为l,若要知道l的值,只要测量图中哪条线段的长( )
A.a B.b C.AD D.AB
【变式18-3】(2020春•北仑区期末)如图,把四张大小相同的长方形卡片(如图①)按图2、图③两种方式放在一个底面为长方形(长比宽多5cm)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为C1,图3中阴影部分的周长为C2,那么C1比C2大 cm.
【考点19 整式的化简求值(化繁为简再求值)】
【例19】(2019秋•沙坪坝区期末)先化简,再求值:2ab+6(12a2b+ab2)﹣[3a2b﹣2(1﹣ab﹣2ab2)],其中a为最大的负整数,b为最小的正整数.
【变式19-1】(2019秋•渝中区校级期末)先化简再求值:3a2b﹣[2ab2﹣2(ab-32a2b)+ab]+3ab2,其中a,b满足(a+4)2+|b-12|=0.
【变式19-2】(2019秋•呼和浩特期末)已知代数式A=﹣6x2y+4xy2﹣2x﹣5,B=﹣3x2y+2xy2﹣x+2y﹣3.
(1)先化简A﹣B,再计算当x=1,y=﹣2时A﹣B的值;
(2)请问A﹣2B的值与x,y的取值是否有关系?试说明理由.
【变式19-3】(2019秋•南开区期末)已知A=a2﹣2b2+2ab﹣3,B=2a2﹣b2-25ab-15.
(1)求2(A+B)﹣3(2A﹣B)的值(结果用化简后的a、b的式子表示);
(2)当|a+12|与b2互为相反数时,求(1)中式子的值.
【考点20 整式的化简求值(整体代入求值)】
【例20】(2019秋•海陵区校级期中)已知A=3x2﹣x+2y﹣4xy,B=x2﹣2x﹣y+xy
(1)求A﹣3B的值.
(2)当x+y=56,xy=﹣1,求A﹣3B的值.
(3)若A﹣3B的值与y的取值无关,求x的值.
【变式20-1】(2019秋•东阿县期末)阅读材料:“如果代数式5a+3b的值为﹣4,那么代数式2(a+b)+4(2a+b)的值是多少?”我们可以这样来解:
原式=2a+2b+8a+4b=10a+6b=2(5a+3b)=2×(﹣4)=﹣8
仿照上面的解题方法,完成下面的问题:
已知3a﹣7b=﹣3,求代数式2(2a+b﹣1)﹣5(4b﹣a)﹣3b的值.
【变式20-2】(2019秋•安庆期末)阅读理解:
如果代数式:5a+3b=﹣4,求代数式2(a+b)+4(2a+b)的值?小颖同学提出了一种解法如下:原式=2a+2b+8a+4b=10a+6b,把式子5a+3b=﹣4两边同时乘以2,得10a+6b=﹣8
仿照小颖同学的解题方法,完成下面的问题:
(1)如果﹣a2=a,则a2+a+1= ;
(2)已知a﹣b=﹣3,求3(a﹣b)﹣5a+5b+5的值;
(3)已知a2+2ab=﹣2,ab﹣b2=﹣4,求2a2+72ab+12b2的值.
【变式20-3】(2019秋•开江县期末)阅读材料:
我们知道,2x+3x﹣x=(2+3﹣1)x=4x,类似地,我们把(a+b)看成一个整体,则2(a+b)+3(a+b)﹣(a+b)=(2+3﹣1)(a+b)=4(a+b).“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(x﹣y)2看成一个整体,求将2(x﹣y)2﹣5(x﹣y)2+(x﹣y)2合并的结果;
(2)已知2m﹣3n=4,求代数式4m﹣6n+5的值;
拓广探索:
(3)已知a﹣2b=5,b﹣c=﹣3,3c+d=9,求(a+3c)﹣(2b+c)+(b+d)的值.
专题1.5 分式章末重难点题型-2021-2022学年八年级数学上册举一反三系列(人教版): 这是一份专题1.5 分式章末重难点题型-2021-2022学年八年级数学上册举一反三系列(人教版),文件包含专题15分式章末重难点题型举一反三人教版解析版docx、专题15分式章末重难点题型举一反三人教版原卷版docx等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
专题1.2 全等三角形章末重难点题型-2021-2022学年八年级数学上册举一反三系列(人教版): 这是一份专题1.2 全等三角形章末重难点题型-2021-2022学年八年级数学上册举一反三系列(人教版),文件包含专题12全等三角形章末重难点题型举一反三人教版解析版docx、专题12全等三角形章末重难点题型举一反三人教版原卷版docx等2份试卷配套教学资源,其中试卷共90页, 欢迎下载使用。
专题1.2 实数章末重难点题型(举一反三)-2021-2022学年七年级下册数学举一反三系列(人教版): 这是一份专题1.2 实数章末重难点题型(举一反三)-2021-2022学年七年级下册数学举一反三系列(人教版),文件包含专题12实数章末重难点题型举一反三人教版解析版doc、专题12实数章末重难点题型举一反三人教版原卷版doc等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。












