(通用版)中考数学一轮复习4.4《全等三角形》精选练习卷(含答案)

这是一份(通用版)中考数学一轮复习4.4《全等三角形》精选练习卷(含答案)，共12页。
1．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A．∠B＝∠C B．AD＝AE C．BD＝CE D．BE＝CD
2．下列各图中a，b，c为三角形的边长，则甲，乙，丙三个三角形和左侧△ABC全等的是( )
A．甲和乙 B．乙和丙 C．甲和丙 D．只有丙
3．如图，△ABC中，AB＝AC，BD＝CE，BE＝CF，若∠A＝50°，则∠DEF的度数是( )
A. 75° B. 70° C. 65° D. 60°
4．如图，AB⊥CD，且AB＝CD.E、F是AD上两点，CE⊥AD，BF⊥AD.若CE＝a，BF＝b，EF＝c，则AD的长为( )
A．a＋c B．b＋c C．a－b＋c D．a＋b－c
5．如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别是点D、E，AD＝3，BE＝1，则DE的长是( )
A.eq \f(3,2) B．2 C．2eq \r(2) D.eq \r(10)
6．在△ABC中，点E，F分别是边AB，AC的中点，点D在BC边上，连接DE，DF，EF，请你添加一个条件________，使△BED与△FDE全等．
7．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC(不添加其他字母及辅助线)，你添加的条件是________．
8．如图，点B，F，C，E在一条直线上，AB∥DE，AC∥DF且AC＝DF，求证：AB＝DE.
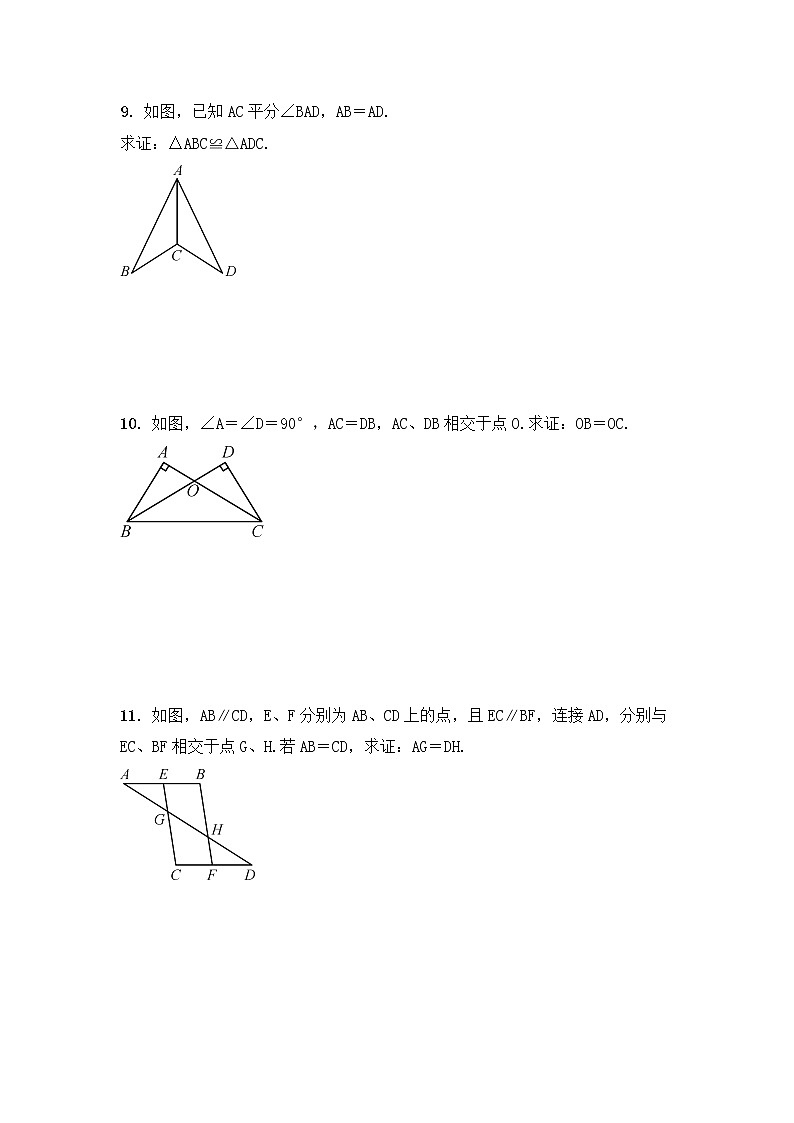
9．如图，已知AC平分∠BAD，AB＝AD.
求证：△ABC≌△ADC.
10．如图，∠A＝∠D＝90°，AC＝DB，AC、DB相交于点O.求证：OB＝OC.
11．如图，AB∥CD，E、F分别为AB、CD上的点，且EC∥BF，连接AD，分别与EC、BF相交于点G、H.若AB＝CD，求证：AG＝DH.
12．如图，△ABC、△CDE均为等边三角形，连接BD、AE交于点O，BC与AE交于点P.
求证：∠AOB＝60°.
13如图，点B、F、C、E在一条直线上，FB＝CE，AB∥ED，AC∥FD，AD交BE于O.
求证：AD与BE互相平分．
14．已知：如图，点A，F，E，C在同一直线上，AB∥DC，AB＝CD，∠B＝∠D.
(1)求证：△ABE≌△CDF；
(2)若点E，G分别为线段FC，FD的中点，连接EG，且EG＝5，求AB的长．
1．如图，点A、D、C、F在同一条直线上，AD＝CF，AB＝DE，BC＝EF.
(1)求证：△ABC≌△DEF；
(2)若∠A＝55°，∠B＝88°，求∠F的度数．
2．如图，已知线段AC，BD相交于点E，AE＝DE，BE＝CE.
(1)求证：△ABE≌△DCE；
(2)当AB＝5时，求CD的长．
3．如图，在△ABC中，AB＝BC，∠ABC＝90°，分别以AB，AC为边在AB同侧作等边△ABD和等边△ACE，连接DE.
(1)判断△ADE的形状，并加以证明；
(2)过图中两点画一条直线，使其垂直平分图中的某条线段，并说明理由．
4．已知：在四边形ABCD中，对角线AC、BD相交于点E，且AC⊥BD，作BF⊥CD，垂足为点F，BF与AC交于点G，∠BGE＝∠ADE.
(1)如图①，求证：AD＝CD；
(2)如图②，BH是△ABE的中线，若AE＝2DE，DE＝EG，在不添加任何辅助线的情况下，请直接写出图②中四个三角形，使写出的每个三角形的面积都等于△ADE面积的2倍．
5．已知，在△ABC中，∠A＝90°，AB＝AC，点D为BC的中点．
(1)如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE＝AF；
(2)若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE＝AF吗？请利用图②说明理由．
参考答案
【基础训练】
1．D 2.B 3.C 4.D 5.B 6.D是BC的中点
7．AC＝BC
8．证明： ∵AB∥DE，AC∥DF，
∴∠B＝∠E，∠ACB＝∠DFE.
在△ABC和△DEF中，
eq \b\lc\{(\a\vs4\al\c1(∠B＝∠E,∠ACB＝∠DFE，,AC＝DF))
∴△ABC≌△DEF(AAS)，∴AB＝DE.
9．证明：∵AC平分∠BAD，
∴∠BAC＝∠DAC，
在△ABC和△ADC中，
eq \b\lc\{(\a\vs4\al\c1(AB＝AD,∠BAC＝∠DAC，,AC＝AC))∴△ABC≌△ADC.
10．证明：在Rt△ABC和Rt△DCB中，eq \b\lc\{(\a\vs4\al\c1(AC＝BD，,CB＝BC，))
∴Rt△ABC≌Rt△DCB(HL)，
∴∠OBC＝∠OCB，
∴BO＝CO.
11．证明： ∵AB∥CD.∴∠A＝∠D.∵EC∥BF.
∴∠BHA＝∠CGD.
∵AB＝CD，
∴△ABH≌△DCG.
∴AH＝DG.∴AG＝DH.
12．证明：∵△ABC、△CDE为等边三角形，
∴∠ACB＝∠ECD＝60°，AC＝BC，CD＝CE，
∴∠ACE＝∠BCD，
在△ACE和△BCD中，
eq \b\lc\{(\a\vs4\al\c1(AC＝BC，,∠ACE＝∠BCD，,CE＝CD，))
∴△ACE≌△BCD(SAS)，∴∠CAE＝∠CBD，
∵∠AOB＋∠CBD＋∠BPO＝180°，
∠BCA＋∠CAE＋∠APC＝180°，
且∠BPO＝∠APC，
∴∠AOB＝∠BCA＝60°.
13.证明：如解图，连接BD，AE，
∵FB＝CE，
∴BC＝EF，
又∵AB∥ED，AC∥FD，
∴∠ABC＝∠DEF，∠ACB＝∠DFE，
在△ABC和△DEF中，
eq \b\lc\{(\a\vs4\al\c1(∠ABC＝∠DEF，,BC＝EF，,∠ACB＝∠DFE，))
∴△ABC≌△DEF(ASA)，∴AB＝DE，
又∵AB∥DE，
∴四边形ABDE是平行四边形，
∴AD与BE互相平分．
14．证明：(1)∵AB∥DC，∴∠A＝∠C.
在△ABE和△CDF中，
eq \b\lc\{(\a\vs4\al\c1(∠A＝∠C，,AB＝CD，,∠B＝∠D，))∴△ABE≌△CDF(ASA)；
(2)解：∵点E，G分别为线段FC，FD的中点，
∴EG＝eq \f(1,2)CD，
∵EG＝5，∴CD＝10，
∵△ABE≌△CDF，
∴AB＝CD＝10.
【拔高训练】
1．(1)证明：∵AC＝AD＋DC，DF＝DC＋CF，且AD＝CF，
∴AC＝DF，
在△ABC和△DEF中，
eq \b\lc\{(\a\vs4\al\c1(AB＝DE,BC＝EF，,AC＝DF))∴△ABC≌△DEF(SSS)；
(2)解：由(1)可知，∠F＝∠ACB.
∵∠A＝55°，∠B＝88°，
∴∠ACB＝180°－(∠A＋∠B)＝180°－(55°＋88°)＝37°，
∴∠F＝∠ACB＝37°.
2．(1)证明：在△AEB和△DEC中，eq \b\lc\{(\a\vs4\al\c1(AE＝DE,∠AEB＝∠DEC，,BE＝EC))
∴△AEB≌△DEC(SAS)．
(2)解：∵△AEB≌△DEC，∴AB＝CD，
∵AB＝5，∴CD＝5.
3．解： (1)△ADE是等腰直角三角形．
理由：在等边△ABD和等边△ACE中，
∵BA＝DA，CA＝EA，∠BAD＝∠CAE＝60°，
∴∠BAD－∠CAD＝∠CAE－∠CAD.
即∠BAC＝∠EAD，
∴△ABC≌△ADE.
∴BC＝DE，∠ABC＝∠ADE，
∵AB＝BC＝AD，∠ABC＝90°，
∴AD＝DE，∠ADE＝90°，
即△ADE是等腰直角三角形．
(2)连接CD，则直线CD垂直平分线段AE.(或连接BE，则直线BE垂直平分线段AC)
理由：由(1)得DA＝DE.
又∵CA＝CE，∴直线CD垂直平分线段AE.
4．(1)证明：∵∠BGE＝∠ADE，∠BGE＝∠CGF，
∴∠ADE＝∠CGF，
∵AC⊥BD，BF⊥CD，
∴∠ADE＋∠DAE＝∠CGF＋∠GCF，
∴∠DAE＝∠GCF，∴AD＝CD.
(2)解：△ACD、△ABE、△BCE、△BHG.
【解法提示】设DE＝a，
则AE＝2DE＝2a，EG＝DE＝a，
∵S△ADE＝eq \f(1,2)AE·DE＝eq \f(1,2)·2a·a＝a2，
∵BH是△ABE的中线，
∴AH＝HE＝a，
∵AD＝CD，AC⊥BD，∴CE＝AE＝2a，
则S△ADC＝eq \f(1,2)AC·DE＝eq \f(1,2)·(2a＋2a)·a＝2a2＝2S△ADE；
在△ADE和△BGE中，
eq \b\lc\{(\a\vs4\al\c1(∠AED＝∠BEG,DE＝GE，,∠ADE＝∠BGE))
∴△ADE≌△BGE(ASA)，∴BE＝AE＝2a，
∴S△ABE＝eq \f(1,2)AE·BE＝eq \f(1,2)·2a·2a＝2a2，
S△BCE＝eq \f(1,2)CE·BE＝eq \f(1,2)·2a·2a＝2a2，
S△BHG＝eq \f(1,2)HG·BE＝eq \f(1,2)·(a＋a)·2a＝2a2，
综上，面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.
5．(1)证明：连接AD，如解图①所示.
第5题解图①
∵∠A＝90°，AB＝AC，
∴△ABC为等腰直角三角形，∠EBD＝45°.
∵点D为BC的中点，
∴AD＝eq \f(1,2)BC＝BD，∠FAD＝45°.
∵∠BDE＋∠EDA＝90°，∠EDA＋∠ADF＝90°，
∴∠BDE＝∠ADF.
在△BDE和△ADF中，
eq \b\lc\{(\a\vs4\al\c1(∠EBD＝∠FAD,BD＝AD，,∠BDE＝∠ADF))
∴△BDE≌△ADF(ASA)，∴BE＝AF.
(2)解：BE＝AF，证明如下：
连接AD，如解图②所示.
第5题解图②
∵∠ABD＝∠BAD＝45°，
∴∠EBD＝∠FAD＝135°.
∵∠EDB＋∠BDF＝90°，∠BDF＋∠FDA＝90°，
∴∠EDB＝∠FDA.
在△EDB和△FDA中，
eq \b\lc\{(\a\vs4\al\c1(∠EBD＝∠FAD,BD＝AD,∠EDB＝∠FDA))，
∴△EDB≌△FDA(ASA)，∴BE＝AF.