浙教版九年级下册1.2 锐角三角函数的计算教学ppt课件

这是一份浙教版九年级下册1.2 锐角三角函数的计算教学ppt课件，文件包含12锐角三角函数的计算2课件pptx、12锐角三角函数的计算2练习docx、12锐角三角函数的计算2学案doc、12锐角三角函数的计算2教案docx等4份课件配套教学资源，其中PPT共14页， 欢迎下载使用。
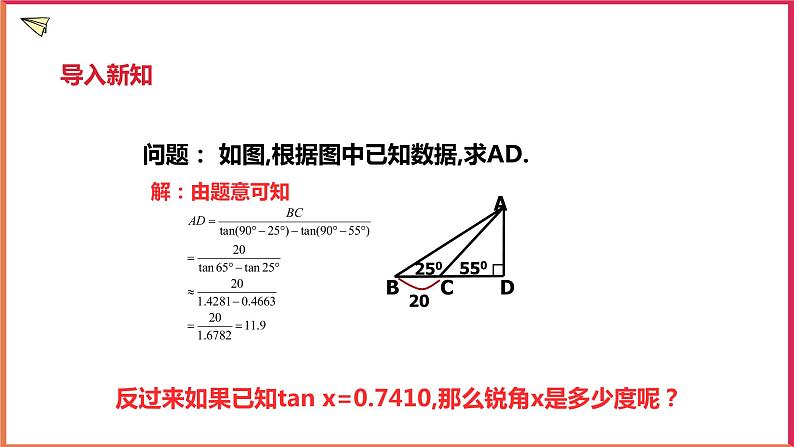
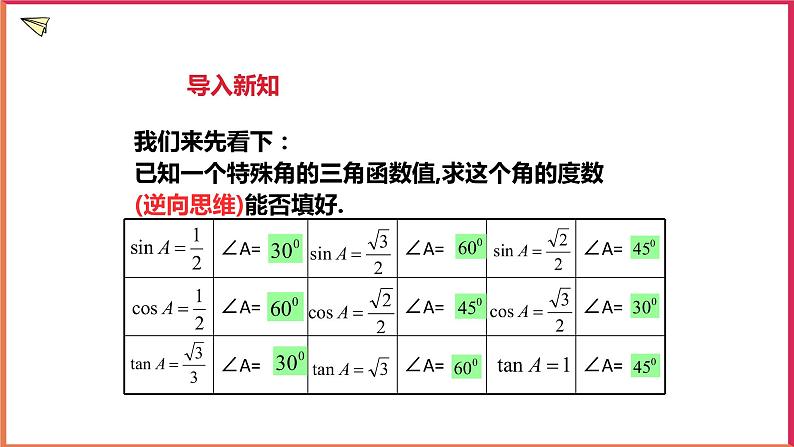
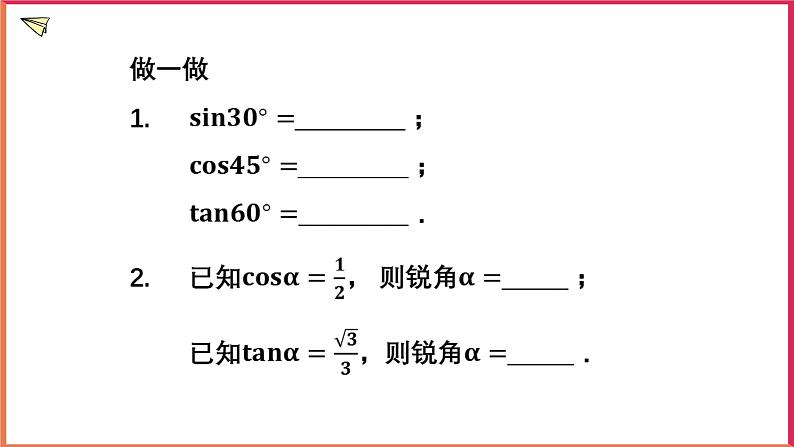
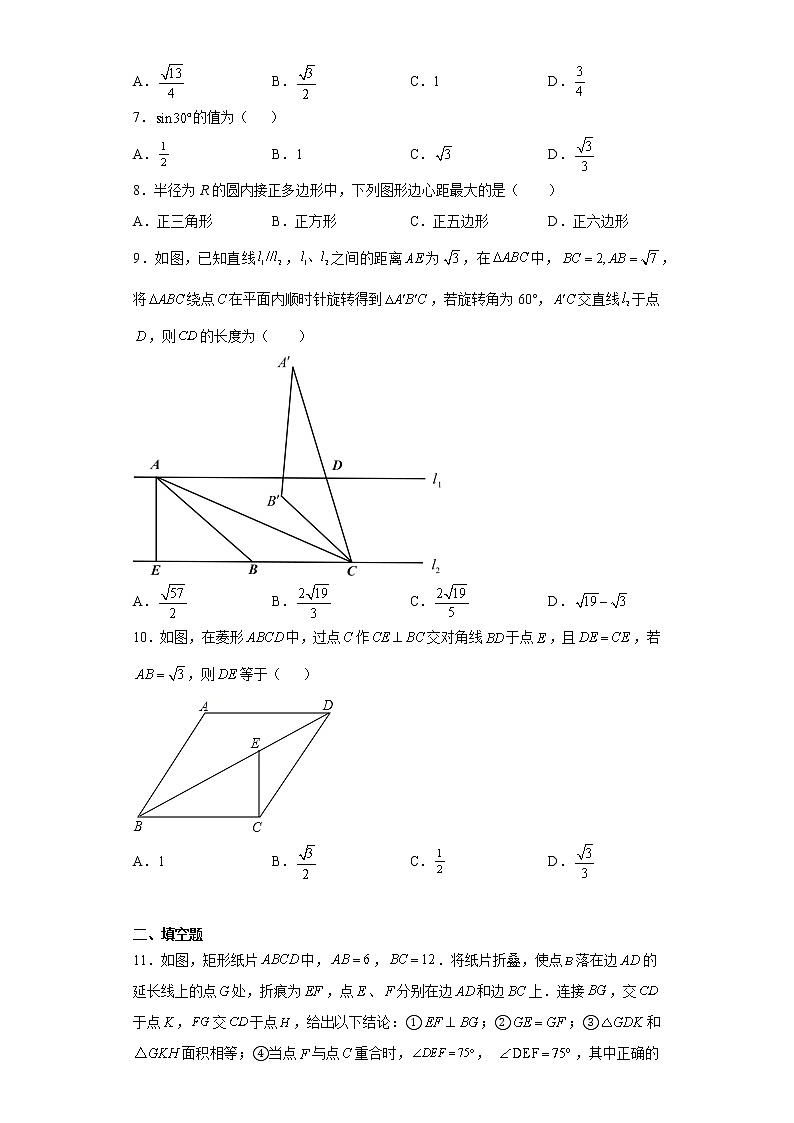
1.2 有关三角函数的计算（2）学习目标1．经历用计算器由已知三角函数值求对应的锐角的过程，更进一步体会三角函数的意义．2．会使用计算器进行由已知三角函数值求对应的锐角的计算，并解决简单的实际问题．重点和难点本节教学的重点是用计算器由已知三角函数值求锐角．例2涉及的知识较多，思路不易形成，是本节教学的难点．学习过程1.创设情景，引入新课问题： 如图,根据图中已知数据,求AD.反过来如果已知tan x=0.7410,那么锐角x是多少度呢？ 2. 复习回顾，巩固已学我们来先看下：已知一个特殊角的三角函数值,求这个角的度数(逆向思维)能否填好.对于不是特殊角的那些三角函数值如何求它们的度数呢？可以利用科学计算器来求吗？如果已知锐角三角函数值，怎样用科学计算器求角的度数呢？ 【做一做】1．sin30°＝；cos45°＝；tan60°＝．2．已知cosα＝，则锐角α＝；已知tanα＝，则锐角α＝．问：由“做一做”可知，已知一个锐角的三角形函数特殊值，可求出相应的特殊角的度数．那么当一个锐角的三角函数值不是特殊值时，如何求这个角的度数呢？例如，已知sinα＝0.2974，如何求锐角呢？已知一个角的三角函数值，求这个角的度数，这类问题可以通过计算器来解决，此时用到“”，“”，“”键的第二功能“”，“”，“”．例如：已知，求锐角．按健顺序为： SHIFT  sin   0   ．   2   9   7   4   ＝ 【例2】根据下面的条件，求锐角的大小（精确到1ʺ）（1）； （2）； （3）．解：（1）β≈26°48ʹ51ʺ；（2）β≈38°12ʹ52ʺ；（3）β≈54°31ʹ55ʺ．介绍用计算器求锐角时，如果学生所用的计算器型号不同，同样可分小组合作学习，让学生根据自己的计算器的按键顺序修改课本中介绍的按键顺序．已知一个角的三角函数值，如果是30°，45°和60°角的三角函数值，应要求学生不用计算器，直接说出它所对应的角，而对于非特殊角的三角函数值，可以用计算器求锐角，如果问题中没有特别说明，通常将计算结果精确到1ʺ．【比一比】已知下列三角函数值，求锐角的大小·(精确到1ʺ）．（1）sinα＝0.6841； sinβ＝0.5136； sinγ＝0.0526．（2）cosα＝0.3241； cosβ＝0.2839； cosγ＝0.5412．（3）tanα＝3.2672； tanβ＝2.3780； tanγ＝57.82．解：（1）α ≈43°9ʹ53ʺ；（2）β ≈30°54ʹ14ʺ；（3）γ ≈3°0ʹ55ʺ．（2）α ≈71°5ʹ20ʺ；（2）β ≈73°30ʹ25ʺ；（3）γ ≈57°14ʹ5ʺ．（3）α ≈72°58ʹ56ʺ；（2）β ≈67°11ʹ32ʺ；（3）γ ≈89°0ʹ33ʺ．【例3】如图，一段公路弯道呈圆弧形，测得弯道两端的距离为200m．的半径为1000m．求弯道的长（精确到0.1m）．解：作OC⊥AB于点C，则OC平分∠AOB．在Rt△OCB中，BC＝AB＝100m，OB＝1000m，则sin∠OBC＝，得≈5.7392，即n≈11.4784．∴l＝≈200.3（m）．答：弯道的长约为200.3m．讲解此例时可进行下述步骤进行（1）以引导学生回顾弧长的计算公式．（2）启发学生把问题归结为只需求圆心角的度数．（3）把问题进一步归结为已知直角三角形的一个锐角的正弦值，求这个锐角．小结时教师可指出从本例可以看到，今后有关弧长和扇形面积的计算问题，不再局限于特殊角的圆心角，半径和弦长之间的互相推算．在Rt△ABC中，∠C＝Rt∠．根据下列条件求各个锐角（精确到1ʹ）．（1）AB＝3，AC＝1．（2）AC＝5，BC＝4．解：（1）∠A＝70°32ʹ，∠B＝19°28ʹ．（2）∠A＝38°40ʹ，∠B＝51°20ʹ．如图，测得一商场自动扶梯的长l为8m，该自动扶梯到达的高度h为5m．问：自动扶梯与地面所成的角θ是多少度（精确到1ʹ）．解：由sinθ＝＝＝0.625，得 θ＝38°41ʹ．答：自动扶梯与地面所成的θ角是38°41ʹ．如图，一个钟摆的摆长OA为1.5m，摆幅（两端的距离）为20cm．求钟摆每摆动一次摆端经过的路程（结果精确到1cm）．解：在Rt△OAC中，∵AC＝10cm＝0.1，OA＝1.5m＝150cm，∴sin∠AOC＝＝＝，∴∠AOC≈3.8°，∴∠AOB＝7.6°，∴＝≈20cm．答：所以钟摆的摆端摆一次经过的路程约为40cm．如图，在Rt△ABC中，∠ACB＝Rt∠，D是AB的中点，tan∠ACD＝．求∠A，∠B的度数（精确到1ʹ）．解：∠A＝18°26ʹ，∠B＝71°34ʹ．