







初中数学浙教版九年级下册1.3 解直角三角形示范课课件ppt
展开
这是一份初中数学浙教版九年级下册1.3 解直角三角形示范课课件ppt,文件包含13解直角三角形1课件pptx、13解直角三角形1练习docx、13解直角三角形1教案doc、13解直角三角形1学案docx等4份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
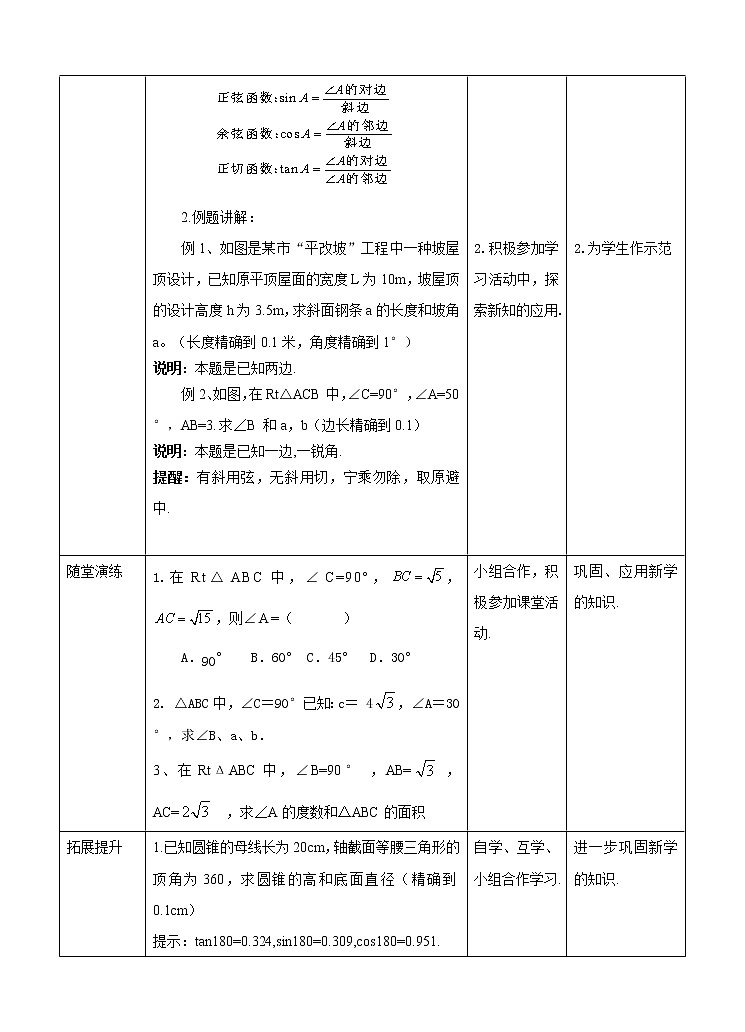
(3)边角之间的关系:sinA=_____,csA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
像这样,在直角三角形中,由已知的一些边、角求出另一些边、角的过程,叫做解直角三角形。
在直角三角形中,都有哪些元素呢?这些元素之间都存怎样的关系呢?
在直角三角形中共有五个元素:边a,b,c, 锐角∠A,∠B.这五个元素之间有如下等量关系:
a2 +b2 =c2 (勾股定理)
在直角三角形中,已知几个元素就可以求出其它元素呢?
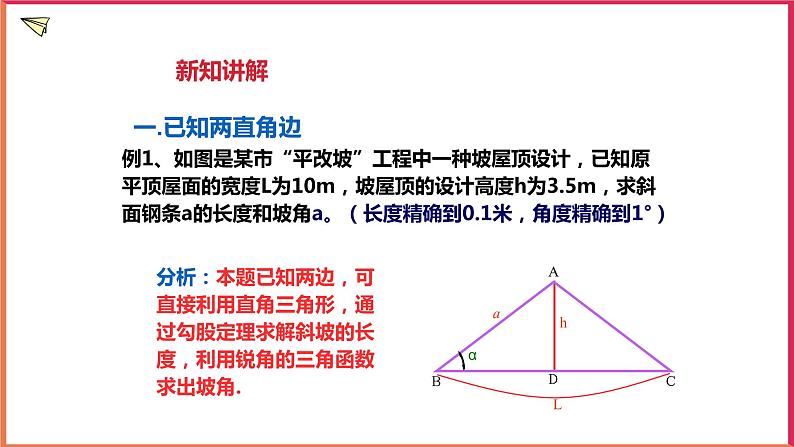
例1、如图是某市“平改坡”工程中一种坡屋顶设计,已知原平顶屋面的宽度L为10m,坡屋顶的设计高度h为3.5m,求斜面钢条a的长度和坡角a。(长度精确到0.1米,角度精确到1°)
分析:本题已知两边,可直接利用直角三角形,通过勾股定理求解斜坡的长度,利用锐角的三角函数求出坡角.
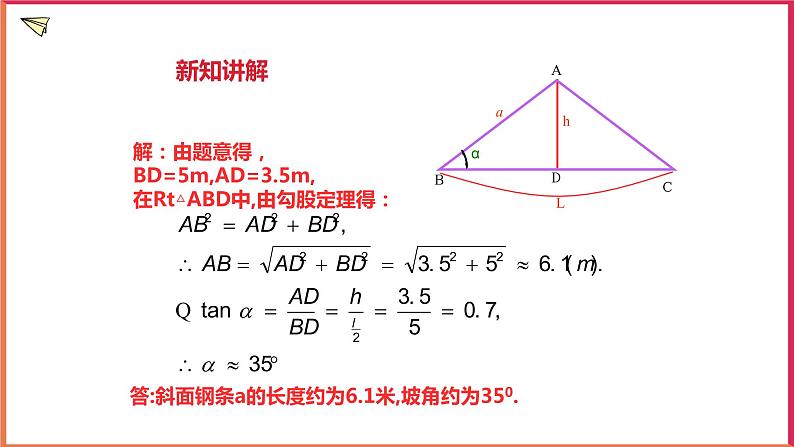
解:由题意得,BD=5m,AD=3.5m,在Rt△ABD中,由勾股定理得:
答:斜面钢条a的长度约为6.1米,坡角约为350.
例2、如图,在Rt△ACB中,∠C=90°,∠A=50 °,AB=3.求∠B 和a,b(边长精确到0.1)
分析:本题根据直角三角形的两个锐角互余求出∠B的度数,接下来运用∠A的正弦和余弦,结合已知条件可求出a和b.
解:在Rt△ACB中, ∠B=90°- 50°=40°,
∴a=AB• sinA=3sin50°≈2.3.
∴b=AB• csA=3cs50°≈1.9.
提醒:有斜用弦,无斜用切,宁乘勿除,取原避中.
在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;(2)已知一条边和一个锐角.
(必须有一个条件是边)
A.90° B.60° C.45° D.30°
2.已知 △ABC中,∠C=90°,c= 4,∠A=30°,求∠B、a、b.
解:由直角三角形两锐角互余得:∠B=∠C -∠A =90°-30°=60°.
∴ a=c• sin 30°=4×0.5=2,
1.已知圆锥的母线长为20cm,轴截面等腰三角形的顶角为360,求圆锥的高和底面直径(精确到0.1cm)
提示:tan180=0.324,sin180=0.309,cs180=0.951.
分析:通过圆锥的母线长为20cm,母线与轴的夹角为30°,求出圆锥的高即得;在RtΔABD中,由csB可得底面半径,进而得直径.
解:如图所示,由题意得:
答:圆锥的高为19.2cm,底面直径为12.4cm.
尝试画出符合题意的图,画出的是直角三角形吗?如果不是要考虑
分析:本题无图,对于无图一般要考虑
解;第一种情况;过A点作 BC边上的高AD,交BC延长线于D,
∵AC=4,∴在RtΔADC中,根据勾股定理得:
解:第二种情况; 过A点作 BC边上的高AD, 交BC于D,
相关课件
这是一份初中数学浙教版九年级下册1.3 解直角三角形课前预习ppt课件,共4页。
这是一份初中1.3 解直角三角形背景图ppt课件,文件包含13解直角三角形3课件pptx、13解直角三角形3练习docx、13解直角三角形3教案doc、13解直角三角形3学案docx等4份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
这是一份浙教版九年级下册1.3 解直角三角形图片课件ppt,文件包含13解直角三角形3课件pptx、13解直角三角形3练习docx、13解直角三角形3教案docx、13解直角三角形3学案doc等4份课件配套教学资源,其中PPT共17页, 欢迎下载使用。










