考点24锐角三角函数及解直角三角形（解析版）-2022年数学中考一轮复习考点透析（北师大版）

考点24锐角三角函数及解直角三角形

【命题趋势】

在锐角三角函数及解直角三角形方面主要考查：1.直角三角形的边与角：①结合平面直角坐标系，网格或利用直角三角形的边角关系求某个角的三角函数值；②已知某个角的三角函数值求线段长。2.解直角三角形的实际应用，以解答题为主，设置背景有：仰角、俯角、方向角、坡比（坡度）及夹角，设置角度有：①求某物的高；②求两点之间的距离，命基础题和中档题。

【常考知识】

1.直角三角形的边与角：①结合平面直角坐标系，网格或利用直角三角形的边角关系求某个角的三角函数值；②已知某个角的三角函数值求线段长。2.解直角三角形的实际应用，以解答题为主，设置背景有：仰角、俯角、方向角、坡比（坡度）及夹角，设置角度有：①求某物的高；②求两点之间的距离。

【夺分技巧】

①求一个角的三角函数值，必须将这个锐角置于直角三角形中，利用锐角三角函数的意义求值。若不是直角三角形中，可以利用相等的角转化或作垂线构造直角三角形。

②巧记300,450,600的函数值。

③在网格中图形中，求一个角的三角函数值往往需要找到以这个角为内角的直角三角形，然后根据勾股定理，算出需要的直角三角形的边长，再根据三角函数的定义求解。

④在解直角三角形的实际问题中，需要添加辅助线将其进行转化。

真题演练

一、单选题

1．（2021·广西港南·九年级期中）若sinα＝，则锐角α＝（　　）

A．30° B．45° C．50° D．60°

【答案】A

【分析】

根据30°角的正弦值等于解答．

【详解】

解：∵sinα＝，

∵锐角α＝30°．

故选：A．

2．（2021·湖北十堰·中考真题）如图，小明利用一个锐角是的三角板测量操场旗杆的高度，已知他与旗杆之间的水平距离为，为（即小明的眼睛与地面的距离），那么旗杆的高度是（    ）

A． B． C． D．

【答案】D

【分析】

先根据题意得出AD的长，在Rt△AED中利用锐角三角函数的定义求出ED的长，由CE＝CD＋DE即可得出结论．

【详解】

解：∵AB⊥BC，DE⊥BC，AD∥BC，

∴四边形ABCD是矩形，

∵BC＝15m，AB＝1.5m，

∴AD＝BC＝15m，DC＝AB＝1.5m，

在Rt△AED中，

∵∠EAD＝30°，AD＝15m，

∴ED＝AD•tan30°＝15×＝5，

∴CE＝CD＋DE＝．

故选：D．

3．（2021·湖南永州·中考真题）下列计算正确的是（    ）

A． B． C． D．

【答案】A

【分析】

根据零指数幂，特殊角三角函数值，算术平方根的定义，同底数幂乘法的计算法则分别计算即可．

【详解】

解：A、，此选项正确；

B、，此选项错误；

C、，此选项错误；

D、，此选项错误；

故选：A．

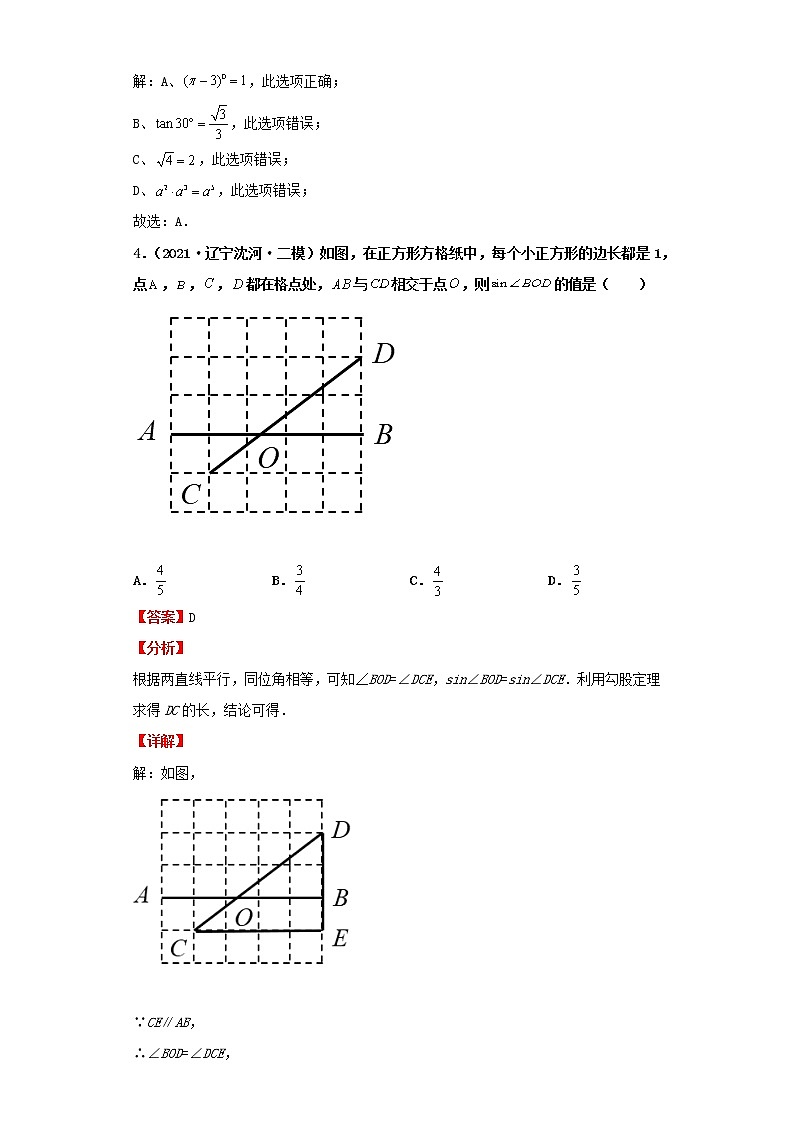
4．（2021·辽宁沈河·二模）如图，在正方形方格纸中，每个小正方形的边长都是1，点，，，都在格点处，与相交于点，则的值是（    ）

A． B． C． D．

【答案】D

【分析】

根据两直线平行，同位角相等，可知∠BOD=∠DCE，sin∠BOD=sin∠DCE．利用勾股定理求得DC的长，结论可得．

【详解】

解：如图，

∵CE∥AB，

∴∠BOD=∠DCE，

∴sin∠BOD=sin∠DCE，

∵CE=4，DE=3，

∴DC==5，

∴sin∠BOD=sin∠DCE=．

故选：D．

5．（2021·山东东营·中考真题）如图，在中，，，，若用科学计算器求AC的长，则下列按键顺序正确的是（    ）

A． B．

C． D．

【答案】D

【分析】

根据正切函数的定义，可得，根据计算器的应用，可得答案．

【详解】

解：由，得：

，

故选：D．

6．（2021·广东深圳·中考真题）计算的值为（    ）

A． B．0 C． D．

【答案】C

【分析】

直接利用特殊角的三角函数值、绝对值的性质分别化简得出答案．

【详解】

故选C．

7．（2021·广东深圳·中考真题）在正方形中，，点E是边的中点，连接，延长至点F，使得，过点F作，分别交、于N、G两点，连接、、，下列正确的是：①；②；③；④（    ）

A．4 B．3 C．2 D．1

【答案】B

【分析】

解：①中由即可得到，再由正切等于对边比邻边即可求解；

②中先证明得到EM=EC，DM=FC，再证明即可求解；

③中先证明GECM，得到即可求解；

④中由得到，再由即可求解．

【详解】

解：①∵，

∴∠DMF=90°=∠NCF，且对顶角∠MND=∠CNF，

∴∠GFB=∠EDC，

∵ABCD为正方形，E是BC的中点，

∴BC=CD，

∴，①正确；

②由①知，

又，已知，

∴()，

∴，

∴，

∵，，，

∴()，

∴，故②正确；

③∵，，

∴BE=ME，

且∠B=∠GME=90°，GE为和的公共边，

∴（），

∴，

∵，

∴，

由三角形外角定理可知：，

∴，

∴，

∴，

∵，，

∴，故③错误；

④由上述可知：，，

∴，

∵，

∴，

∴，故④正确．

故选B．

8．（2021·广东·广州市第二中学二模）下列各式正确的是（    ）

A． B．

C． D．

【答案】D

【分析】

直接根据特殊的锐角三角函数值、幂的乘方、二次根式的运算、以及同底数指数幂相除的运算法则进行计算即可；

【详解】

A、 ，故该选项错误；

B、 ，故该选项错误；

C、 无意义，根号下的数不能是负数，故该选项错误；

D、 ，故该选项正确；

故选：D．

9．（2021·四川内江·中考真题）如图，菱形的顶点分别在反比例函数和的图象上，若，则的值为（   ）

A． B． C． D．

【答案】D

【分析】

连接AC、BD，根据菱形的性质和反比例函数的对称性，即可得出∠BOC=90°，∠BCO=∠BCD=30°，解直角三角形求得，作 BM⊥x轴于M，CN⊥x轴于N，证得△OMB∽△CNO，得到，根据反比例函数系数 k的几何意义即可求得结果．

【详解】

解：连接、，

四边形是菱形，

，

菱形的顶点分别在反比例函数和的图象上，

与、与关于原点对称，

、经过点，

，

，

，

作轴于，轴于，

，

，

，

，

，

，

，

故选：．

10．（2021·安徽·合肥一六八中学模拟预测）如图所示，有一山坡在水平方向每前进100m就升高60m，那么山坡的坡度为（   ）

A． B． C． D．

【答案】A

【分析】

根据坡度是坡面的铅直高度h和水平宽度l的比计算即可．

【详解】

解：铅直高度为，水平宽度为，

山坡的坡度，

故选．

二、填空题

11．（2021·宁夏·银川市第三中学一模）如图是某水库大坝横断面示意图．其中、分别表示水库上下底面的水平线，，的长是，则水库大坝的高度是______．（结果保留根号）

【答案】

【分析】

过点C作于点E，得到，在中，利用正弦定义解题即可．

【详解】

解：过点C作于点E，

在中，

的长是

m，

故答案为：．

12．（2021·江苏·高港实验学校二模）某人沿着坡度i＝1：的山坡走到离地面25米高的地方，则他走的路程为____米．

【答案】50

【分析】

根据题意，作出图形，再根据坡度可以求得此为30°的直角三角形，根据性质即可求解．

【详解】

解：根据题意，如下图：

由题意可知：，

坡度i＝1：可知，

∴

∴

故答案为50

13．（2021·广东·佛山市华英学校一模）如图，直立于地面上的电线杆AB，在阳光下落在水平地面和坡面上的影子分别是BC， CD．测得BC=9m，CD=6m，斜坡CD的坡度i=1:，在D处哵得电线杆顶端A的仰角为30°，则电线杆AB的高度为______．（结果保留根号）

【答案】6+3

【分析】

延长AD交BC的延长线于F，作DG⊥BF于G，根据直角三角形的性质和勾股定理求出DC、CG的长，根据正切的定义解答即可．

【详解】

解：如图，延长AD交BC的延长线于F，作DG⊥BF于G，

∵∠ADE=30°，

∴∠AFB=30°，

∵CD=6m，斜坡CD的坡度i=1：，

∴tan∠DCG=，

∴∠DCG=30°，

∴DG=3m，CG=3m，

∴∠DFC=∠DCF=30°，

∴DF=DC，

∵DG⊥BF，

∴FG=CG=3（m），

∴FC=6m，

∴FB=FC+BC=（6+9）m，

∴AB=BF×tan∠AFB=（6+9）×=（6+3）m．

故答案为：6+3．

14．（2021·全国·九年级课时练习）计算：＝______________．

【答案】

【分析】

根据特殊角的锐角三角函数值，零次幂，负整指数幂进行计算即可．

【详解】

故答案为：

15．（2021·辽宁丹东·中考真题）已知：到三角形3个顶点距离之和最小的点称为该三角形的费马点．如果是锐角（或直角）三角形，则其费马点P是三角形内一点，且满足．（例如：等边三角形的费马点是其三条高的交点）．若，P为的费马点，则_________；若，P为的费马点，则_________．

【答案】5       

【分析】

①作出图形，过分别作,勾股定理解直角三角形即可

②作出图形，将绕点逆时针旋转60，P为的费马点则四点共线，即，再用勾股定理求得即可

【详解】

①如图,过作，垂足为,

过分别作, 则, P为的费马点

5

②如图：

.

将绕点逆时针旋转60

由旋转可得：

是等边三角形，

P为的费马点

即四点共线时候，

=

故答案为：①5，②

16．（2021·广东·东莞市东华初级中学模拟预测）如图，半径为的中，为直径，弦且过半径的中点，点为上一动点，于点．当点从点出发顺时针运动到点时，点所经过的路径长为_______________．

【答案】

【分析】

根据题意,当点从点出发顺时针运动到点,点的路径是以为半径，中点为圆心的一段圆弧，求出圆心角和半径即可求得弧长，即点所经过的路径长．

【详解】

点的路径是以为半径，中点为圆心的一段圆弧

如图，连接，设于点，连接的中点和点,

的半径为,弦且过半径的中点，为直径

,

,

故答案为：．

17．（2021·江西九江·二模）如图设计一张折叠型方桌子，若，，将桌子放平后，要使AB距离地面的高为40cm，则两条桌腿需要叉开的应为____________．

【答案】120°

【分析】

作DE⊥AB于E．在Rt△ADE中，可得，即可求得∠DAB=30°，再利用等腰三角形的性质及三角形的内角和定理即可求得∠AOB=120°．

【详解】

作DE⊥AB于E．

∴AD=50+30=80cm，DE=40cm，

在Rt△ADE中，，

∴∠DAB=30°，

∵，

∴∠AOB=180°-30°-30°=120°．

故答案为：120°．

三、解答题

18．（2021·全国·九年级专题练习）先化简，再求代数式的值，其中．

【答案】，．

【分析】

先运用特殊角的三角函数求出x，然后化简分式，最后代入计算即可．

【详解】

解：，

=

=

=

=

=；

当x=时，．

19．（2021·山东青岛·中考真题）某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼的高度．如图所示，其中观景平台斜坡的长是20米，坡角为，斜坡底部与大楼底端的距离为74米，与地面垂直的路灯的高度是3米，从楼顶测得路灯项端处的俯角是．试求大楼的高度．

（参考数据：，，，，，）

【答案】96米

【分析】

延长AE交CD延长线于M，过A作AN⊥BC于N，则四边形AMCN是矩形，得NC=AM，AN=MC，由锐角三角函数定义求出EM、DM的长，得出AN的长，然后由锐角三角函数求出BN的长，即可求解．

【详解】

延长交于点，

过点作，交于点，

由题意得，，

∴四边形为矩形，

∴，.

在中，，

∴，，

∴，，

∴，

∴.

在中，，

∴，

∴，

∴，

∴.

答：大楼的高度约为96米.

20．（2021·内蒙古新城·二模）如图1，在Rt△ABC中，∠ABC＝90°，AB是⊙O的直径，⊙O交AC于点D，过点D的直线交BC于点E，交AB的延长线于点P，∠A＝∠PDB．

（1）求证：PD是⊙O的切线；

（2）若AB＝6，DA＝DP，试求的长；

（3）如图2,点M是弧AB的中点,连接DM，交AB于点N，若tanA＝，求的值．

【答案】（1）证明见解析；（2）；（3）

【分析】

（1）连接OD根据AB是圆的直径得到∠ADB=90°，∠A+∠OBD=90°再根据∠A=∠PDB，∠OBD=∠ODB即可证明；

（2）根据DA=DP得到∠A=∠P，再根据∠A=∠PDB，∠DBA=∠P+∠PDB即可求得∠A进而得到∠DOB，再根据弧长公式求解即可得到答案；

（3）连接OM，OD，过D作DF⊥AB于F，设BD=2x，则AD=3x利用三角函数和勾股定理可以得到，然后证明，利用相似三角形的性质求解即可得到答案.

【详解】

解：（1）如图所示，连接OD

∵AB是圆的直径

∴∠ADB=90°

∴∠A+∠OBD=90°

∵OD=OB

∴∠OBD=∠ODB

∴∠A+∠ODB=90°

又∵∠A=∠PDB

∴∠PDB+∠ODB=90°

∴∠PDO=90°

∴PD⊥OD

∴PD是圆的切线；

（2）∵DA=DP

∴∠A=∠P

∵∠A=∠PDB

∴∠A=∠PDB=∠P

∵∠DBA=∠P+∠PDB

∴∠DBA=2∠A

∵AB是圆的直径

∴∠ADB=90°，

∴∠A+∠OBD=90°

∴3∠A=90°

∴∠A=30°

∴∠DOB=60°

∴

（3）如图所示，连接OM，OD，过D作DF⊥AB于F

∵点M是弧AB的中点

∴OM⊥AB

∵

∴

设BD=2x，则AD=3x

∵

∴，

∴

∵DF⊥AB，OM⊥AB

∴DF∥OM

∴

∴

21．（2021·四川内江·中考真题）在一次课外活动中，某数学兴趣小组测量一棵树的高度．如图所示，测得斜坡的坡度，坡底的长为8米，在处测得树顶部的仰角为，在处测得树顶部的仰角为，求树高．（结果保留根号）

【答案】米．

【分析】

作BF⊥CD于点F，设DF=x米，在直角△DBF中利用三角函数用x表示出BF的长，在直角△DCE中表示出CE的长，然后根据BF-CE=AE即可列方程求得x的值，进而求得CD的长．

【详解】

解：作于点，设米，

在中，，

则（米，

∵，且AE=8

∴

∴

在直角中，米，

在直角中，，

米．

，即．

解得：，

则米．

答：的高度是米．