初中数学第一章 三角形的证明3 线段的垂直平分线优秀ppt课件

这是一份初中数学第一章 三角形的证明3 线段的垂直平分线优秀ppt课件，共27页。PPT课件主要包含了学习目标，导入新课，讲授新课，想一想，∵PAPB，利用三角形的全等证明，当堂检测，30°，①②③，∴DECE等内容，欢迎下载使用。
1.探索证明线段垂直平分线的性质和判定.2.能运用线段垂直平分线性质和其判定解决实际问题.3.经历“探索-发现-猜想-证明”的过程，进一步体会证明的必要性，增强证明意识和能力，发展推理能力.
1 线段是轴对称图形吗？它的对称轴是什么？
2 什么叫线段的垂直平分线？
3 线段的垂直平分线有什么性质？
经过某一条线段的中点，并且垂直于这条线段的直线，这条线段的垂直平分线(中垂线).
垂直平分线性质：线段垂直平分线上的点到这条线段两个端点的距离相等．
某区政府为了方便居民的生活，计划在三个住宅小区A、B、C之间修建一个购物中心，试问该购物中心应建于何处，才能使得它到三个小区的距离相等？
垂直底边，并且平分底边．
AD所在的直线即线段BC的垂直平分线 ．
等腰三角形顶角平分线有哪些性质？
垂直且平分一条线段的直线是这条线段的垂直平分线.
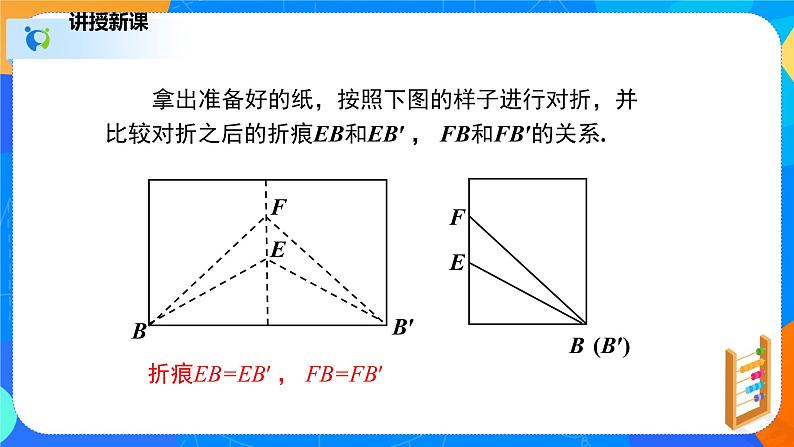
拿出准备好的纸，按照下图的样子进行对折，并比较对折之后的折痕EB和EB′ ， FB和FB′的关系.
折痕EB=EB′ ， FB=FB′
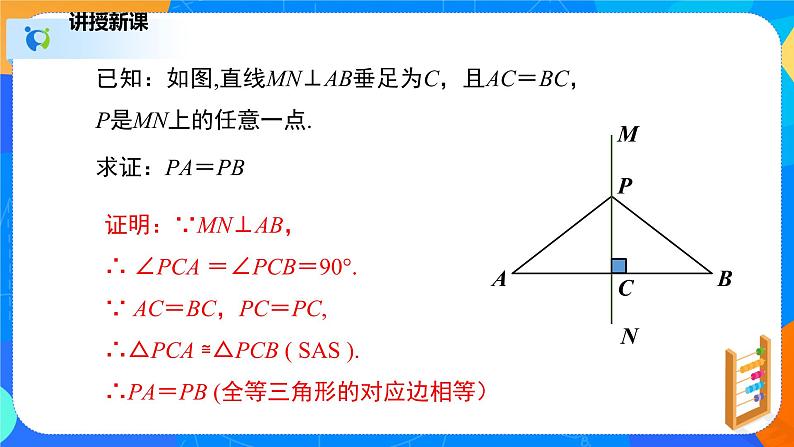
已知：如图,直线MN⊥AB垂足为C，且AC＝BC，P是MN上的任意一点.求证：PA＝PB
证明：∵MN⊥AB，∴ ∠PCA ＝∠PCB＝90°.∵ AC＝BC，PC＝PC,∴△PCA ≌△PCB ( SAS ). ∴PA＝PB (全等三角形的对应边相等）
1．性质：线段垂直平分线上的点到这条线段两个端点的距离相等；条件：点在线段的垂直平分线上；结论：这个点到线段两端点的距离相等．表达方式：如图，l⊥AB，AO＝BO，点P在l上，则AP＝BP.2．作用：可用来证明两线段相等．
例1 如图，在△ABC中，AC＝5，AB的垂直平分线DE交AB，AC于点E，D.若△BCD的周长为8，求BC的长；
解：∵DE是AB的垂直平分线，∴AD＝BD.∴BD＋CD＝AD＋CD＝AC＝5.∵△BCD的周长为8，∴BC＝△BCD的周长－(BD＋CD)＝8－5＝3.
你能写出上面这个定理的逆命题吗?它是真命题吗?
定理：线段垂直平分线上的点到这条线段两个端点的距离相等
一个点在线段的垂直平分线上
这个点到线段两端的距离相等
一个点到线段两端的距离相等
这个点在线段的垂直平分线上
想一想：如果PA=PB,那么点P是否在线段AB的垂直平分线上呢？
（1）当点P在线段AB上时，
∴点P为线段AB的中点，
显然此时点P在线段AB的垂直平分线上；
（2）当点P在线段AB外时，如右图所示.
∴△PAB是等腰三角形.
过顶点P作PC⊥AB，垂足为点C，
∴底边AB上的高PC也是底边AB上的中线.
即 PC⊥AB，且AC=BC.
∴直线PC是线段AB的垂直平分线，
此时点P也在线段AB的垂直平分线上.
1．判定：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．2．条件：点到线段两端点距离相等；3．结论：点在线段垂直平分线上．4．表达方式：如图，∵PA＝PB，∴点P在线段AB的垂直平分线上．5．作用：①作线段的垂直平分线的依据；②可用来证线段垂直、相等．
用尺规作线段的垂直平分线已知：线段AB．求作：线段AB的垂直平分线．
作法：1.分别以点A和B为圆心，以大于AB的一半长为半径画弧，两弧相交于点C和D；2.连接直线CD．直线CD就是线段AB的垂直平分线．
例2：已知：如图△ABC中，AB=AC，O是△ABC内一点，且OB=OC.求证：直线AO垂直平分线段BC.
证明：∵AB=AC， ∴A在线段BC的垂直平分线（到一条线段两个端点距离相等的点，在这条线段的垂直平分线上）.同理，点O在线段BC的垂直平分线.∴直线AO是线段BC的垂直平分线（两点确定一条直线）.
证明：延长AO交BC于点D，∵AB＝AC， AO＝AO， OB＝OC ，∴△ABO≌△ACO（SSS）.∴∠BAO=∠CAO，∵AB=AC，∴AO⊥BC．∵OB＝OC ，OD＝OD ，∴RT△DBO≌RT△DCO（HL）.∴BD＝CD.∴直线AO垂直平分线段BC.
1. 如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是 (　 　)
A.AB=AD　 B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC
2.如图，在△ABC中，AC的垂直平分线交AB于点D，DC平分∠ACB，若∠A=50°，则∠B的度数为（ ）
A.25° B.30 °C.35 ° D.40 °
3. 如图,在△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是(　 　)A.8B.9C.10D.11
4. 如图,在四边形ABCD中,E为AB的中点,DE⊥AB于点E, ∠A=66°, ∠ABC=90°, BC=AD,则∠C的大小为______. 
5.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_________. 
6. 如图所示，在△ABC中，BC=8cm,边AB的垂直平分线交AB于点D，交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
7.下列说法：①若点P、E是线段AB的垂直平分线上两点，则EA＝EB，PA＝PB；②若PA＝PB，EA＝EB，则直线PE垂直平分线段AB；③若PA＝PB，则点P必是线段AB的垂直平分线上的点；④若EA＝EB，则经过点E的直线垂直平分线段AB．其中正确的有 （填序号）.
8.两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有　　　(填序号).①AC⊥BD;②AC,BD互相平分;③CA平分∠BCD.
9.已知：如图，点E是∠AOB的平分线上一点，EC⊥OA, ED⊥OB,垂足分别为C,D，连接CD.求证：OE是CD的垂直平分线.
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴ OE是CD的垂直平分线.
在Rt△EDO和Rt△ECO中，ED＝EC，OE＝OE∴Rt△EDO≌Rt△ECO（HL）.∴OD＝OC∴O，E都在CD的垂直平分线上，
10..如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.求证:AB∥DF.
证明:∵EF垂直平分BD,∴FB=FD,∴∠FBD=∠BDF,∵BD是∠ABC的平分线,∴∠ABD=∠FBD,∴∠ABD=∠BDF,∴AB∥DF.
11.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于　　　　.
解：根据△ABC中∠A为锐角与钝角,分为两种情况:①当∠A为锐角时,∵AB的垂直平分线与AC所在的直线相交所得到锐角为50°,∴∠A=40°,∴∠B= =70°;
②当∠A为钝角时,∵AB的垂直平分线与AC所在的直线相交所得到锐角为50°,∴∠1=40°,∴∠BAC=140°,∴∠B=∠C= =20°.综上所述，∴∠B等于70°或20°.
线段的垂直平分线的性质和判定
到线段的两个端点距离相等的点在线段的垂直平分线上
线段的垂直平分线上的点到线段的两个端点的距离相等
见垂直平分线，得线段相等
判断一个点是否在线段的垂直平分线上