初中数学人教版九年级上册24.1.3 弧、弦、圆心角说课ppt课件

这是一份初中数学人教版九年级上册24.1.3 弧、弦、圆心角说课ppt课件，共46页。

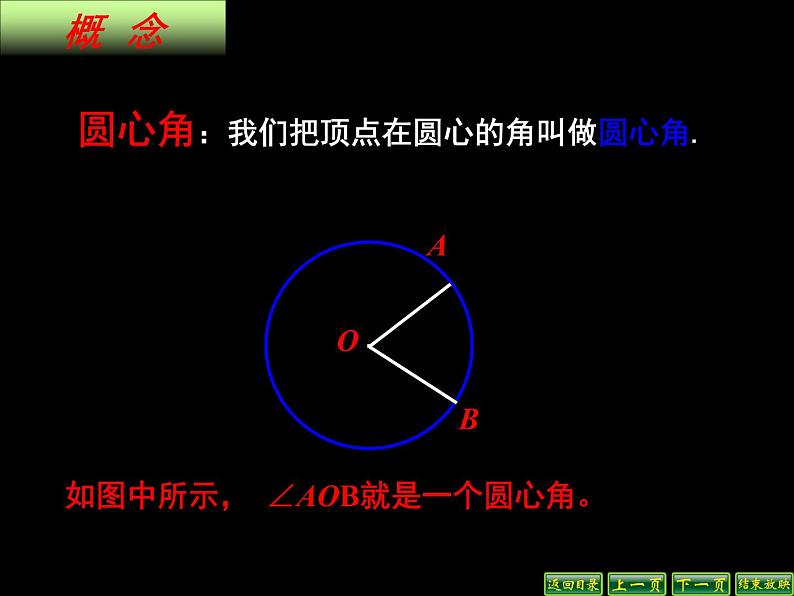
圆心角：我们把顶点在圆心的角叫做圆心角.
如图中所示， ∠AOB就是一个圆心角。
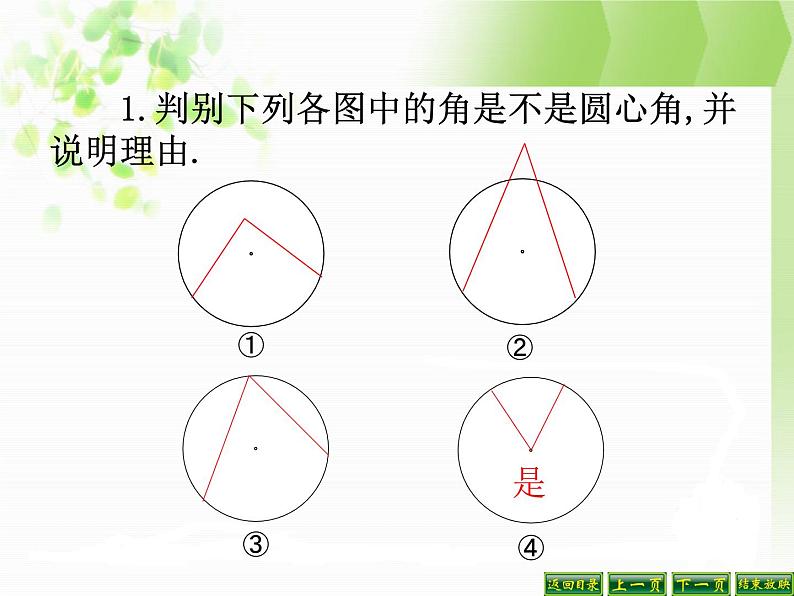
1.判别下列各图中的角是不是圆心角,并说明理由.
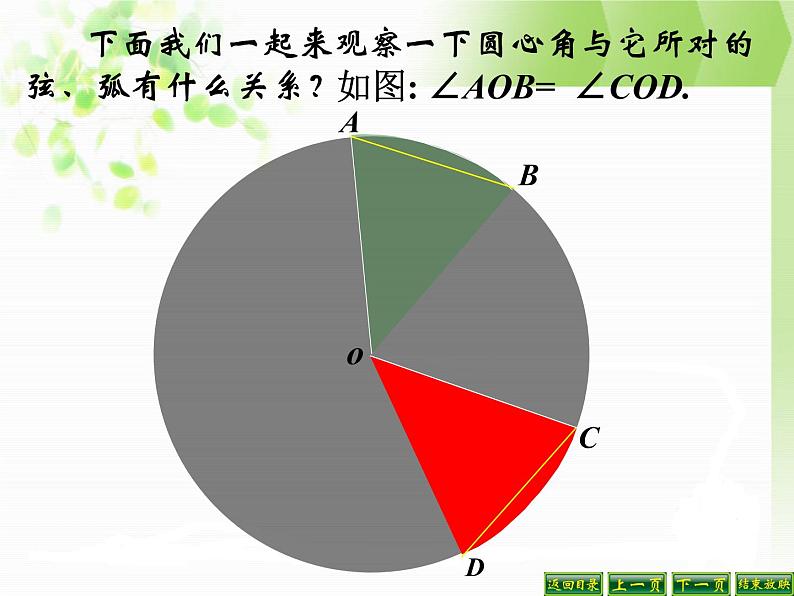
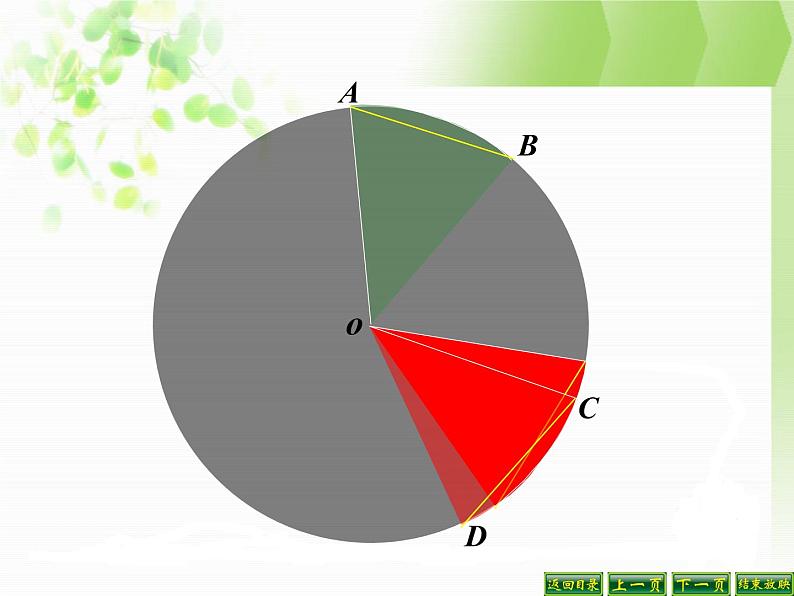
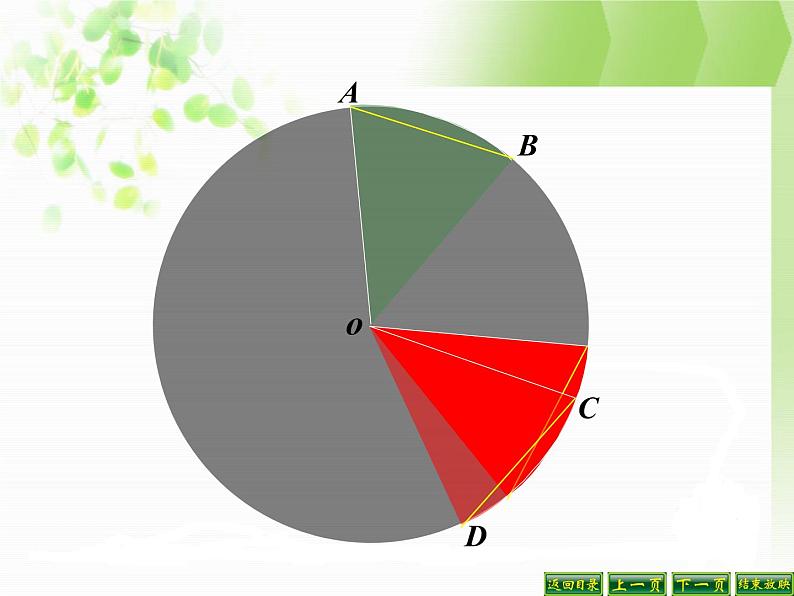
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图: ∠AOB= ∠COD.
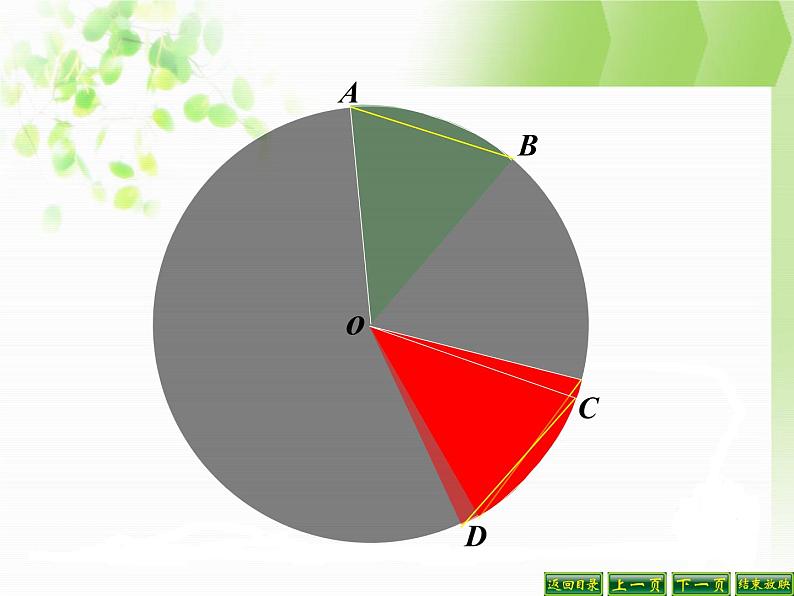
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图:∠AOB =∠COD
∵∠AOB=∠COD,∴射线OA和射线OC重合，射线OB和射线OD重合，又∵同圆的半径相等，∴半径OA与OC重合,半径OB和半径OD重合∴点A与点C重合,点B与点D重合.∴AB=CD，弧AB与弧CD重合.
定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦也相等.
圆心角,弧,弦之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等，所对的弦也相等.
由条件:①∠AOB=∠A′O′B′
在同圆或等圆中,如果轮换下面三组条件: ①两个圆心角,②两条弧,③两条弦,你能得出什么结论?与同伴交流你的想法和理由.
①∠AOB=∠A′O′B′
在同圆或等圆中如果圆心角相等
在同圆或等圆中如果弦相等
弦所对的弧(指劣弧)相等
在同圆或等圆中如果弧相等
推论:(圆心角定理的逆定理) 在同圆或等圆中,如果两个圆心角、两条弧或两条弦中有一组量相等,那么它们所对应的其余的各组量都分别相等.
下面的说法正确吗?为什么?如图,因为
根据圆心角、弧、弦的关系定理可知：
不正确,因为不在同圆或等圆中.
∴ AB=AC, △ABC 等腰三角形．
∴ △ABC是等边三角形， ∴ AB=BC=CA.
∴ ∠AOB＝∠BOC＝∠AOC.
例1、 如图在⊙O中，AB=AC ，∠ACB=60°，求证:∠AOB=∠BOC=∠AOC.
1.如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么___________，_________________．（2）如果 = ，那么____________，______________．（3）如果∠AOB=∠COD，那么_____________，____________．（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？
相 等
因为AB=CD ，所以∠AOB=∠COD.
又因为AO=CO，BO=DO，
所以△AOB ≌ △COD.
又因为OE 、OF是AB与CD对应边上的高，
所以 OE = OF.
2、如图:已知OA,OB是⊙O中的两条半径,且OA⊥OB,D是弧AB上的一点,AD的延长线交OB延长线于点C.已知∠C=25°,求圆心角∠DOB的度数.
3.如图，AB是⊙O的直径， , ∠COD=35°，求∠AOE的度数．
∵把圆心角等分成360份,则每一份的圆心角是1º.同时整个圆也被分成了360份.
则每一份这样的弧叫做1º的弧.
这样,1º的圆心角对着1º的弧, 1º的弧对着1º的圆心角. n º的圆心角对着nº的弧, n º的弧对着nº的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
例2、如图，在⊙O中，弦AB所对的劣弧为圆的 ，圆的半径为4cm，求AB的长