北师大版2 平方根课文ppt课件

这是一份北师大版2 平方根课文ppt课件，共21页。PPT课件主要包含了复习回顾，－329，用符号表示平方根，什么数才有平方根，非负数，a≥0，巩固提高，课时小结，课后作业等内容，欢迎下载使用。
1、什么叫算术平方根？
若一个正数x的平方等于a，即x2=a，则称x为a的算术平方根。x可以用_____表示
只有 才有算术平方根。
（1） = ；
（2） = ；
如果一个数的平方等于9，这个数是什么？
因此，如果一个数的平方等于9，那么这个数是3或－3。
我们把9称为3或－3的平方，那么我们把3或－3叫做9的什么呢？
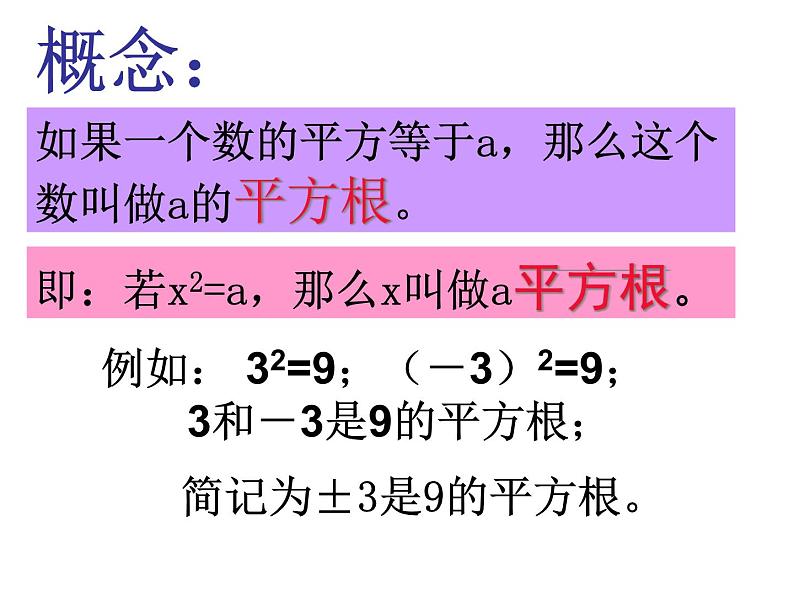
如果一个数的平方等于a，那么这个数叫做a的平方根。
即：若x2=a，那么x叫做a平方根。
例如： 32=9；（－3）2=9；
3和－3是9的平方根；
简记为±3是9的平方根。
正数a的算术平方根记作
所以,正数a的平方根可表以示为：
这样求一个正数的平方根，只要求出它的算术平方根，在前面添上“±”，就是它的平方根了。
例如： =9，则81的平方根是±9， 即：± =±9。
已知x2=a,若知x求a,这种运算叫 ;那么,知a求x,这种运算又叫做什么呢?
求一个数a的平方根的运算，叫开平方。
例： ±3的平方等于9，9的平方根是±3。
所以，平方与开平方互为逆运算。
例1：求下列各数的平方根。
∴100的平方根是±10
∴ 的平方根是±
∴0.25的平方根是±0.5
根据定义x2=a，那么x叫做a平方根。
只有 才有平方根。
正数的平方根有什么特点？0的平方根是多少？负数有平方根吗？
其中， 就是这个数的算术平方根。
因为02=0，所以0的平方根是0。
因为任何一个数的平方都不会是负数，所以负数没有平方根。
举例：（ ）2=16
正数的平方根有 ；
它们 ；
看出:16的平方根有两个,分别是4和－4,它们互为相反数。而且，4就是16的算术平方根。
正数有 个平方根，它们 ；
0的平方根是 ；
负数 ；
例：判断下列各数有没有平方根。 如果有，求出它的平方根；如果没有，说明理由。
（－7）2的平方根是±7。
∵－72=－49，负数没有平方根。
例 求下列各式的值：
1、求下列各数的平方根；
2、计算下列各式的值：
1、求下列各式中x的值：
（3）（x-2）2=4
（3）解：x-2=±2
（1）（-5）2的平方根是 ，算术平方根 是 ；
（4）已知 有意义,则x一定是 .
（5）若一个数的一个平方根为-7，则另一个平方根为 ，这个数是 。
（6）若一个正数的两个平方根为2a-6、3a+1，则a= ，这个正数为 ；
（7）平方根等于本身的数是 ，算术平方根等于它本身的数是 ，算术平方根和平方根相等的数是 ；
1、若x2=a，那么x叫做a平方根。正数a的平方根可表以示为：
2、求一个数a的平方根的运算，叫开平方。 平方与开平方互为逆运算。
3、正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根。4.
课本P29 3,4,5