北师大版九年级下册期末测试题含解析答案

这是一份北师大版九年级下册期末测试题含解析答案，文件包含期末测试02原卷版doc、期末测试02解析版doc等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

姓名：___________考号：___________分数：___________
（考试时间：100分钟 满分：120分）
选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的）
1．如图，在矩形ABCD中，DE⊥AC垂足为F，交BC于点E，BE=2EC，连接AE．则tan∠CAE的值为（ ）
A．B．C．D．
2．如图，在菱形中，，，，则tan∠的值是( )
A．B．2C．D．
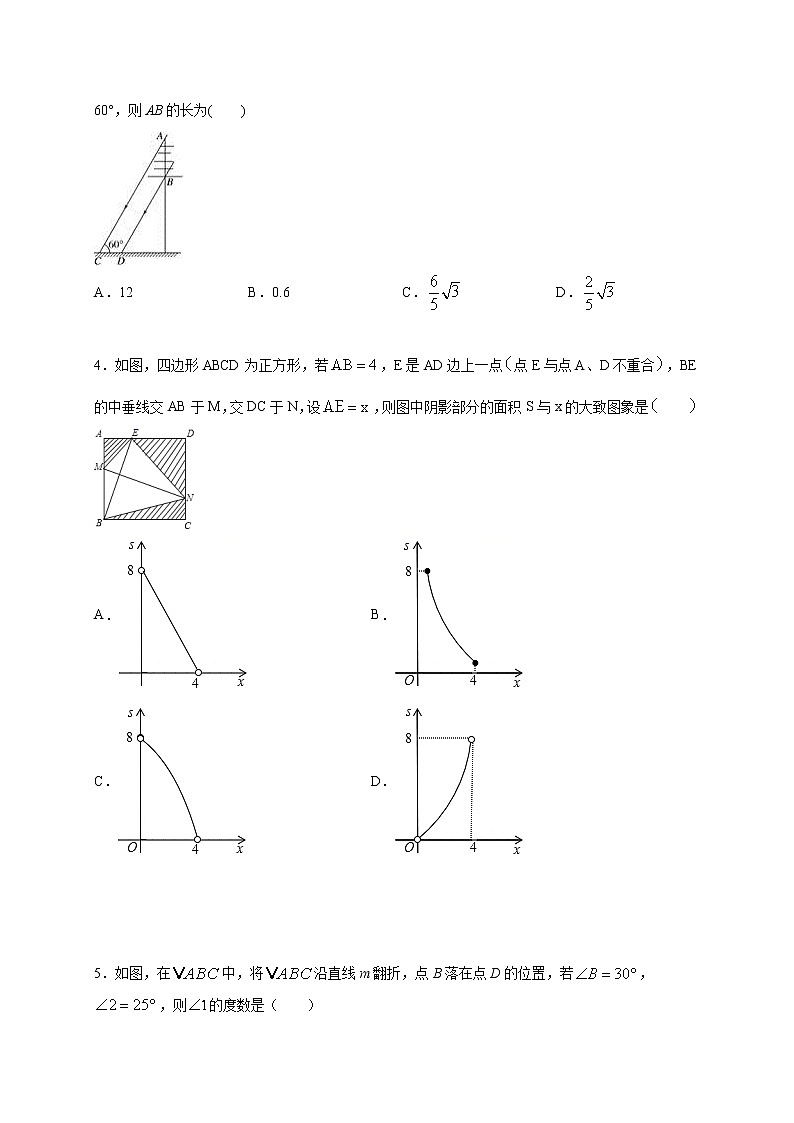
3．一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2，太阳光线与地面的夹角∠ACD＝60°，则AB的长为( )
A．12B．0.6C．D．
4．如图，四边形ABCD为正方形，若，E是AD边上一点点E与点A、D不重合，BE的中垂线交AB于M，交DC于N，设，则图中阴影部分的面积S与x的大致图象是
A．B．
C．D．
5．如图，在中，将沿直线m翻折，点B落在点D的位置，若，，则的度数是（ ）
A．B．C．D．
6．已知点在抛物线上，则的大小关系是（ ）
A．B．C．D．
7．如图，是的直径，弦，，，则阴影部分的面积为（ ）
A．B．C．D．
8．已知△ABC的外心为O，连结BO，若∠OBA=18°，则∠C的度数为（ ）
A．60°B．68°C．70°D．72°
9．如图，等边三角形ABC内接于⊙O，若边长为4cm，则⊙O的半径为（ ）
A．6cmB．4cmC．2cmD．2cm
10．已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，有下列5个结论：
①abc>0;②b>a+c；③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
A．2个B．3个C．4个D．5个
11．二次函数为常数，且)中的与的部分对应值如表：
下列结论错误的是( )
A．B．是关于的方程的一个根；
C．当时，的值随值的增大而减小；D．当时，
12．如图，在平面直角坐标系中，已知点A(0，1)、B(0，3)、C(0，-1)、D(4，4)，点P为平面内一点且满足PC⊥PB，则线段PD的最大值为（ ）
A．10B．8C．7D．9
二、填空题（本大题共6小题，每小题3分，共18分）
13．计算：______．
14．将抛物线向左平移个单位，再向上平移个单位，则平移后的抛物线的表达式为_____________________．
15．如图，在△ABC中，BC=AC=4，∠ACB =90°，点M是边AC的中点，点P是边AB上的动点，则PM+PC的最小值为_______.
16．如图，线段 AB 是⊙O 的直径，弦 CD⊥AB，AB=8，∠CAB=22.5°，则 CD的长等于___________________________．
17．如图，在矩形中，以点为圆心，长为半径作弧，交于点连接过点作垂足为点，再以点为圆心，长为半径作弧，交于点，若，则图中阴影部分面积为___________________．
18．二次函数的图象如图，则方程的解为_______．
三、解答题（本大题共6小题，共66分，解答应写出文字说明、演算步骤或推理过程）
19．如图，已知AB是⊙O的直径，C是⊙O上的一点，D是AB上的一点，DE⊥AB于D，DE交BC于F，且EF＝EC．
（1）求证：EC是⊙O的切线；
（2）若BD＝4，BC＝8，圆的半径OB＝5，求切线EC的长．
20．如图，五泉山的两个景点、处于同一水平地面上，一架无人机在空中沿方向水平飞行进行航拍作业，与在同一铅直平面内，当无人机飞行至处时，测得景点的俯角为，景点的俯角为，测得、之间的距离为100米，求景点、之间的距离．（结果保留整数，参考数据：，，，）
21．已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高．
（1）求证：AC·BC＝BE·CD；
（2）已知CD＝6、AD＝3、BD＝8，求⊙O的直径BE的长．
22．如图1，抛物线y＝ax2+bx+2与x轴交于A，B两点，与y轴交于点C，AB＝4，矩形OBDC的边CD＝1，延长DC交抛物线于点E．
（1）求抛物线的解析式；
（2）如果点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M，A，C，N为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M的坐标；若不存在，请说明理由．
23．如图，抛物线y=ax2+bx+c与x轴的交点分别为A（﹣6，0）和点B（4，0），与y轴的交点为C（0，3）．
（1）求抛物线的解析式；
（2）点P是线段OA上一动点（不与点A重合），过P作平行于y轴的直线与AC交于点Q，点D、M在线段AB上，点N在线段AC上．
①是否同时存在点D和点P，使得△APQ和△CDO全等，若存在，求点D的坐标，若不存在，请说明理由；
②若∠DCB=∠CDB，CD是MN的垂直平分线，求点M的坐标．
24．如图，抛物线过，两点，点，关于抛物线的对称轴对称，过点作直线轴，交轴于点．

（1）求抛物线的表达式；
（2）点是抛物线上一动点，且位于第四象限，当的面积为6时，求出点的坐标；
（3）若点在直线上运动，点在轴上运动，当以点，，为顶点的三角形为等腰直角三角形时称这样的点为“美丽点”，共有多少个“美丽点”？请直接写出当点为“美丽点”时，的面积。···
···
···
···