2021学年10.1 随机事件与概率课堂检测

这是一份2021学年10.1 随机事件与概率课堂检测，共19页。试卷主要包含了0分），【答案】C，【答案】D，【答案】A，【答案】B等内容，欢迎下载使用。

10.1随机事件与概率同步练习人教 A版（2019）高中数学必修二
一、单选题（本大题共12小题，共60.0分）
1. 小明打开计算机时，忘记了开机密码的前两位，只记得第一位是M,I,N中的一个字母，第二位是1，2，3，4，5中的一个数字，则小明输入一次密码能够成功开机的概率是(    )
A. B. 18 C. D.
2. 从一箱产品中随机地抽取一件，设事件A={抽到一等品}，事件B={抽到二等品}，事件C={抽到三等品}，且已知P(A)=0.65，P(B)=0.2，P(C)=0.1.则事件“抽到的不是一等品”的概率为(  )
A. 0.7 B. 0.65 C. 0.35 D. 0.3
3. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果，哥德巴赫猜想的内容是：每个大于2的偶数都可以表示为两个素数的和，例如：10=5+5=3+7(其中3+7与7+3算同一种方法)，在大于4且不超过16的偶数中，随机选取两个不同的偶数，则两个偶数都可以有两种方法表示为两个素数的和的概率为(   )
A. 45 B. 35 C. 12 D. 15
4. 甲、乙两人每人可以用手出0，5，10三种数字，同时可以喊0，5，10，15，20五种数字，当两人所出数字之和等于某人所喊数字时为胜，若甲喊10，乙喊15，则(    )
A. 甲胜的概率大 B. 乙胜的概率大
C. 甲、乙胜的概率一样大 D. 不能确定
5. 现有甲、乙、丙、丁4名学生平均分成两个志愿者小组到校外参加两项活动，则乙、丙两人恰好参加同一项活动的概率为(   )
A. 12 B. 13 C. 16 D. 112
6. 已知随机事件A和B互斥，且P(A∪B)=0.7，P(B)=0.2，则P(A)=(  )
A. 0.5 B. 0.1 C. 0.7 D. 0.8
7. 对空中飞行的飞机连续射击两次，每次发射一枚炮弹，设A={两次都击中飞机}，B={两次都没击中飞机}，C={恰有一次击中飞机}，D={至少有一次击中飞机}，下列关系不正确的是(    )
A. A⊆D B. B∩D=⌀ C. A∪C=D D. A∪B=B∪D
8. 已知函数f(x)=12ax2+bx+1，其中a∈{2,4}，b∈{1,3}，则f(x)在上是减函数的概率为(    )
A. 12 B. 34 C. 16 D. 0
9. 有一种“棒打老虎”游戏．游戏由两个人同时喊出“棒子，老虎，鸡，虫”其中之一，规定：棒子胜老虎，老虎胜鸡，鸡胜虫，虫胜棒子，其余情况不分胜负．甲乙两人进行一次这样的游戏，则甲胜乙的概率为(    )
A. 18 B. 14 C. 13 D. 12
10. 先后2次抛掷一枚骰子，将得到的点数分别记为a，b，两次点数互不影响，设三条线段的长分别为a，b和5，求这三条线段能围成等腰三角形(含等边三角形)的概率为(     )
A. 736 B. 1136 C. 49 D. 718
11. 在抽查作业的试验中，下列各组事件都是基本事件的是(   )
A. 抽到第一组与抽到第二组 B. 抽到第一组与抽到男学生
C. 抽到女学生与抽到班干部 D. 抽到班干部与抽到学习标兵
12. 如果事件A，B互斥，且A，B分别为事件A，B的对立事件，那么(      )
A. A+B是必然事件 B. A+B是必然事件
C. A与B一定互斥 D. A与B一定不互斥
二、单空题（本大题共3小题，共15.0分）
13. 某篮球队员在比赛中每次罚球的命中率相同，且在两次罚球中至多命中一次的概率为1625，则该队员每次罚球的命中率为          ．
14. 国庆节放假，甲、乙、丙三人去北京旅游的概率分别是13，14，15.假定三人的行动相互之间没有影响，那么这段时间内至少有1人去北京旅游的概率为          ．
15. 已知射手甲射击一次，命中9环以上(含9环)的概率为0.5，命中8环的概率为0.2，命中7环的概率为0.1，则甲射击一次，命中6环以下(含6环)的概率为          ．
三、多空题（本大题共3小题，共15.0分）
16. 已知三个事件A，B，C两两互斥且P(A)=0.3，P(B)=0.6，P(C)=0.2，则P(A)=          ，P(A⋃B⋃C)=          ．
17. 已知向量a=(x,−1)，b=(3,y)，其中x随机选自集合{−1,1，3}，y随机选自集合{1,3，9}。则满足a // b的概率为          ;满足a⊥b的概率为          ．
18. 一个袋子中有5个红球，4个绿球，8个黑球，如果随机地摸出一个球，记事件A={摸出黑球}，事件B={摸出绿球}，事件C={摸出红球}，则P(B)=          ，P(AUC)=          
四、解答题（本大题共5小题，共60.0分）
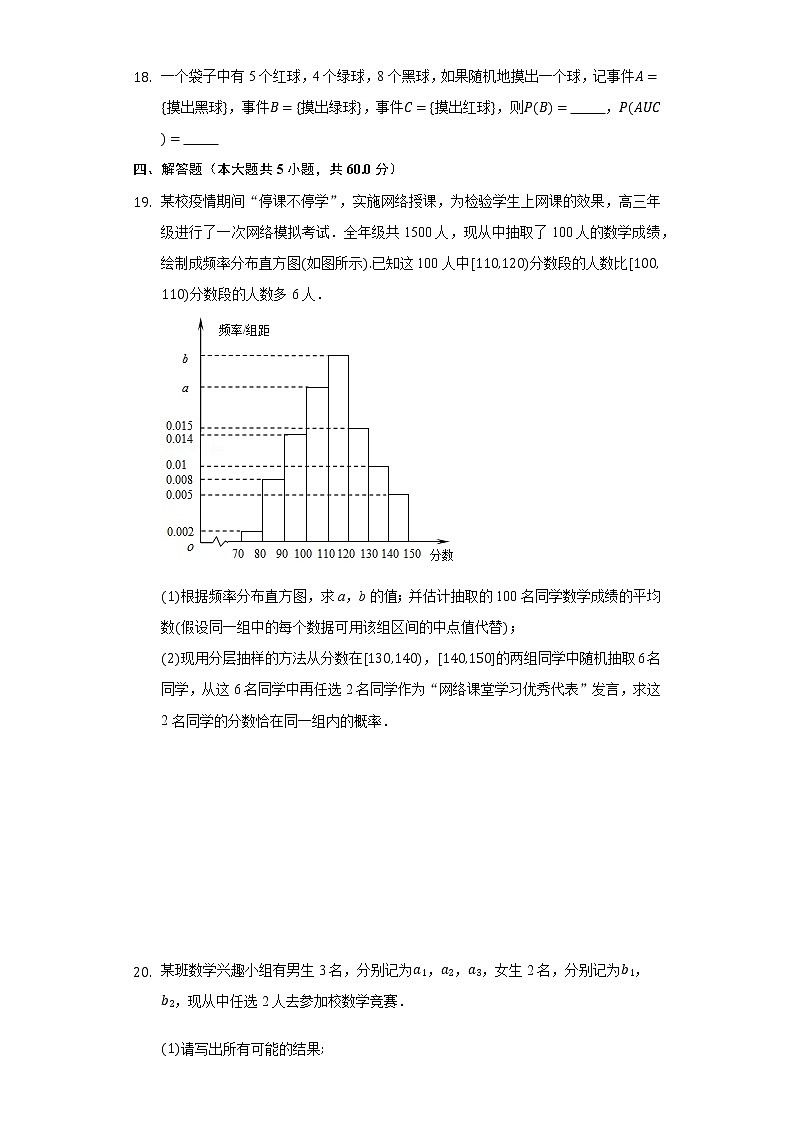
19. 某校疫情期间“停课不停学”，实施网络授课，为检验学生上网课的效果，高三年级进行了一次网络模拟考试．全年级共1500人，现从中抽取了100人的数学成绩，绘制成频率分布直方图(如图所示).已知这100人中[110,120)分数段的人数比[100,110)分数段的人数多6人．

(1)根据频率分布直方图，求a，b的值；并估计抽取的100名同学数学成绩的平均数(假设同一组中的每个数据可用该组区间的中点值代替)；
(2)现用分层抽样的方法从分数在[130,140)，[140,150]的两组同学中随机抽取6名同学，从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言，求这2名同学的分数恰在同一组内的概率．







20. 某班数学兴趣小组有男生3名，分别记为a1，a2，a3，女生2名，分别记为b1，b2，现从中任选2人去参加校数学竞赛．
(1)请写出所有可能的结果;
(2)求参赛学生中恰有1名男生的概率;
(3)求参赛学生中至少有1名男生的概率．







21. 已知袋中装有5个小球，其中3个黑球记为A，B，C，2个红球记为a，b，现从中随机摸出两个球．
(1)写出所有的基本事件；
(2)求两个球中恰有一个黑球的概率；
(3)求两个球中至少有一个黑球的概率．







22. 为了解某地区中学生的身体发育状况，拟采用分层抽样的方法从甲、乙、丙三所中学抽取6个教学班进行调查．已知甲、乙、丙三所中学分别有12，6，18个教学班．
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数；
(Ⅱ)若从抽取的6个教学班中随机抽取2个进行调查结果的对比，求这2个教学班中至少有1个来自甲学校的概率．







23. 某校社团活动深受学生欢迎，每届高一新生都踊跃报名加入．现已知高一某班60名同学中有4名男同学和2名女同学参加摄影社，在这6名同学中，2名同学初中毕业于同一所学校，其余4名同学初中毕业于其他4所不同的学校.现从这6名同学中随机选取2名同学代表社团参加校际交流(每名同学被选到的可能性相同)．
(1)在该班随机选取1名同学，求该同学参加摄影社的概率；
(2)求从这6名同学中选出的2名同学代表恰有1名女同学的概率； 
(3)求从这6名同学中选出的2名同学代表来自于不同的初中学校的概率．







答案和解析
1.【答案】C

【解析】
【分析】
本题考查随机事件发生的概率，关键是列举基本事件总数时不重不漏，是基础题．
列举出从M，I，N中任取一个字母，再从1，2，3，4，5中任取一个数字的基本事件数，然后由随机事件发生的概率得答案．
【解答】
解：从M，I，N中任取一个字母，再从1，2，3，4，5中任取一个数字，
取法总数为：
(M,1)，(M,2)，(M,3)，(M,4)，(M,5)，(I,1)，(I,2)，(I,3)，(I,4)，(I,5)，(N,1)，(N,2)，(N,3)，(N,4)，(N,5)共15种．
其中只有一个是小明的密码前两位．
由随机事件发生的概率可得，小明输入一次密码能够成功开机的概率是115．
故选：C．
  
2.【答案】C

【解析】
【分析】
根据对立事件的概率和为1，结合题意，即可求出结果．
本题考查了求互斥事件与对立事件的概率的应用问题，是基础题．
【解答】
解：由题意，对立事件的概率和为1，
∵事件A={抽到一等品}，且 P(A)=0.65，
∴事件“抽到的不是一等品”的概率为
P=1−P(A)=1−0.65=0.35．
故选：C．
  
3.【答案】D

【解析】
【分析】
本题考查了古典概型的计算与应用，属于拔高题．
采用列举法可得总的情况有15个，满足要求的只有3个，根据概率公式即可得到答案．
【解答】
解：在大于4且不超过16的偶数中6=3+3，8=3+5，10=3+7=5+5，12=5+7，14=3+11=7+7，16=3+13=5+11，
其中，可以有两种方法表示为两个素数的和的偶数有10，14，16．
从大于4且不超过16的偶数中，随机选取两个不同的偶数的所有情况有：(6,8)，(6,10)，(6,12)，(6,14)，(6,16)，(8,10)，(8,12)，(8,14)，(8,16)，(10,12)，(10,14)，(10,16)，(12,14)，(12,16)，(14,16)，共15种．
其中两个偶数都可以有两种方法表示为两个素数的和的情况有(10,14)，(10,16)，(14,16)，共3种．
所以由古典概型得两个偶数都可以有两种方法表示为两个素数的和的概率为P=315=15，
故选 D．
  
4.【答案】A

【解析】
【分析】
本题考查古典概型的计算，属拔高题．
总的事件个数9个，列举出甲或乙胜的情况，利用古典概型的概率公式计算．
【解答】
解：甲、乙两人猜拳，每人可以用手出0，5，10三种数字，共有3×3=9种可能，
若甲猜10，甲胜的情况有：甲用手出0，乙用手出10；或甲用手出5，乙用手出5；甲用手出10，乙用手出0；共3种，
则甲胜的概率为39=13；
若乙猜15时，乙胜的情况有：甲用手出5，乙用手出10；甲用手出10，乙用手出5；共2种，
乙胜的概率为29；
∴乙