数学人教A版 (2019)5.6 函数 y=Asin（ ωx ＋ φ）教学ppt课件

这是一份数学人教A版 (2019)5.6 函数 y=Asin（ ωx ＋ φ）教学ppt课件，共48页。PPT课件主要包含了内容索引，课前篇自主预习，课堂篇探究学习，课标阐释，思维脉络，知识点拨，微判断，答案D，答案C，解列表如下等内容，欢迎下载使用。
1.会用“五点法”画出函数y=Asin(ωx+φ)的图象.(直观想象)2.能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响.(数学抽象)3.掌握函数y=sin x与y=Asin(ωx+φ)图象间的变换关系,能正确地指出其变换步骤.(逻辑推理)
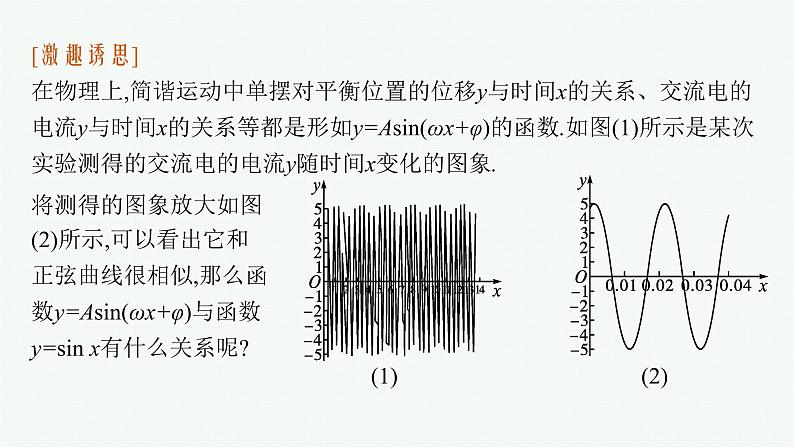
[激趣诱思]在物理上,简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y=Asin(ωx+φ)的函数.如图(1)所示是某次实验测得的交流电的电流y随时间x变化的图象.
将测得的图象放大如图(2)所示,可以看出它和正弦曲线很相似,那么函数y=Asin(ωx+φ)与函数y=sin x有什么关系呢?
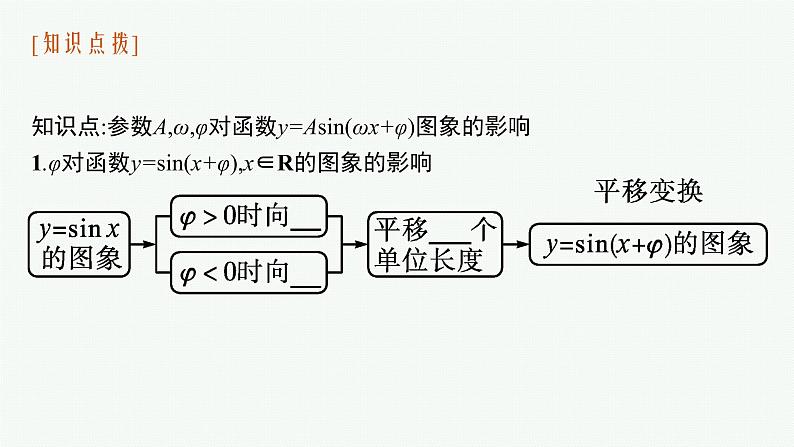
知识点:参数A,ω,φ对函数y=Asin(ωx+φ)图象的影响1.φ对函数y=sin(x+φ),x∈R的图象的影响
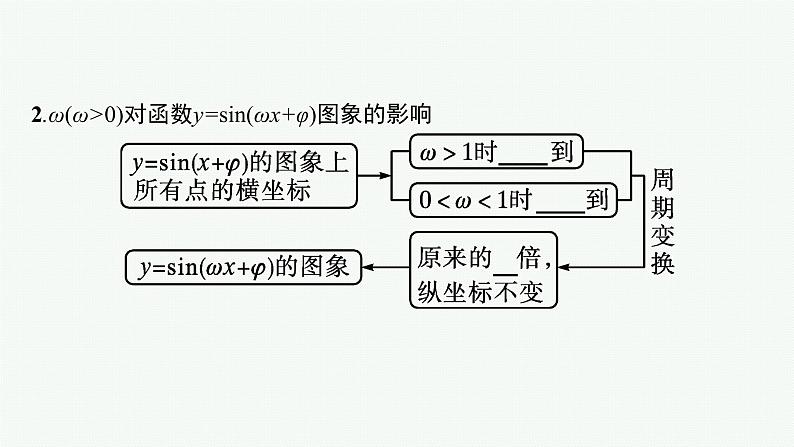
2.ω(ω>0)对函数y=sin(ωx+φ)图象的影响
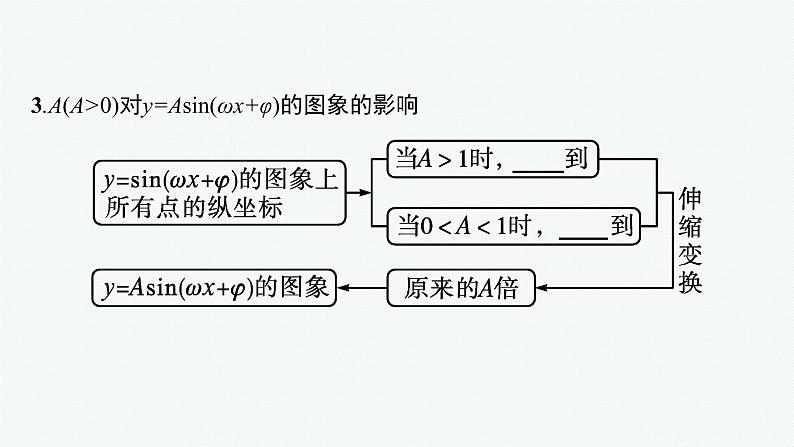
3.A(A>0)对y=Asin(ωx+φ)的图象的影响
名师点析 由y=sin x的图象得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种方法:
(2)y=sin x的图象上所有点的横坐标都变为原来的2倍所得图象的解析式是y=sin 2x.(　　)(3)y=sin x的图象上所有点的纵坐标都变为原来的2倍所得图象的解析式是y= sin x.(　　)答案 (1)×　(2)×　(3)×
微练习(1)把函数y=2sin 3x的图象上所有点的横坐标变为原来的2倍,纵坐标变为原来的3倍,得到　　　　的图象. (2)将函数y=cs 2x的图象向右平移 个单位长度,所得图象对应的解析式为　　　　. 
例1一个大风车的半径为6 m,12 min旋转一周,它的最低点P0离地面2 m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间m(min)之间的函数关系式是(　　)
反思感悟 匀速圆周运动的数学模型一般都归结为正弦型或余弦型函数形式.此类问题的切入点是初始位置及其半径、频率的值要明确,半径决定了振幅A,频率或周期能确定ω,初始位置不同对φ有影响.还要注意最大值与最小值与函数中参数的关系.
描点连线(如图所示).
反思感悟 1.“五点法”作图的实质利用“五点法”作函数y=Asin(ωx+φ)的图象,实质是利用函数的三个零点及两个最值点画出函数在一个周期内的图象.2.用“五点法”作函数y=Asin(ωx+φ)图象的步骤第一步:列表.第二步:在同一平面直角坐标系中描出各点.第三步:用光滑曲线连接这些点,得到图象.
反思感悟 1.对函数y=Asin(ωx+φ)+k(A>0,ω>0,φ≠0,k≠0),其图象的基本变换有:(1)振幅变换(纵向伸缩变换):是由A的变化引起的,A>1时伸长,A1时缩短,ω0时左移,φ0时上移,k0,ω>0,φ≠0,k≠0)的图象得到y=sin x的图象,可采用逆向思维,将原变换反过来逆推得到.
(2)若将函数f(x)=3sin(2x+φ)(0