2021届山西省阳泉市高三理数三模试卷及答案

这是一份2021届山西省阳泉市高三理数三模试卷及答案，共9页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
 高三理数三模试卷一、单项选择题1.集合 ，且 有16个子集，那么实数a可以是〔    〕            A. -1                                           B. 0                                           C. 2                                           D. 32.i为虚数单位，复数 ，那么z在复平面内对应的点位于〔    〕            A. 第一象限                           B. 第二象限                           C. 第三象限                           D. 第四象限3.为考察A､B两名运发动的训练情况，下面是A､B两名运发动连续10天完成训练指标任务的综合得分的折线图，给出以下四个结论，其中错误的结论是〔    〕  A. 第3天至第10天两名运发动综合得分均超过80分
B. 第2天至第7天B运发动的得分逐日提高
C. 第2天至第3天A运发动的得分增量大于B运发动的得分增量
D. A运发动第1天至第3天的得分方差大于第2天至第4天的得分的方差4.双曲线 ，圆 与双曲线C的一条渐近线相交所得弦长为2，那么双曲线的离心率等于〔    〕            A.                                        B.                                        C.                                        D. 5.在平面直角坐标系中，将不等式组 表示的平面区域绕 轴旋转一周所形成的几何体的体积是〔    〕            A.                                         B.                                         C.                                         D. 6.函数 〔 且 〕的大致图像是〔    〕            A.                                     B. 
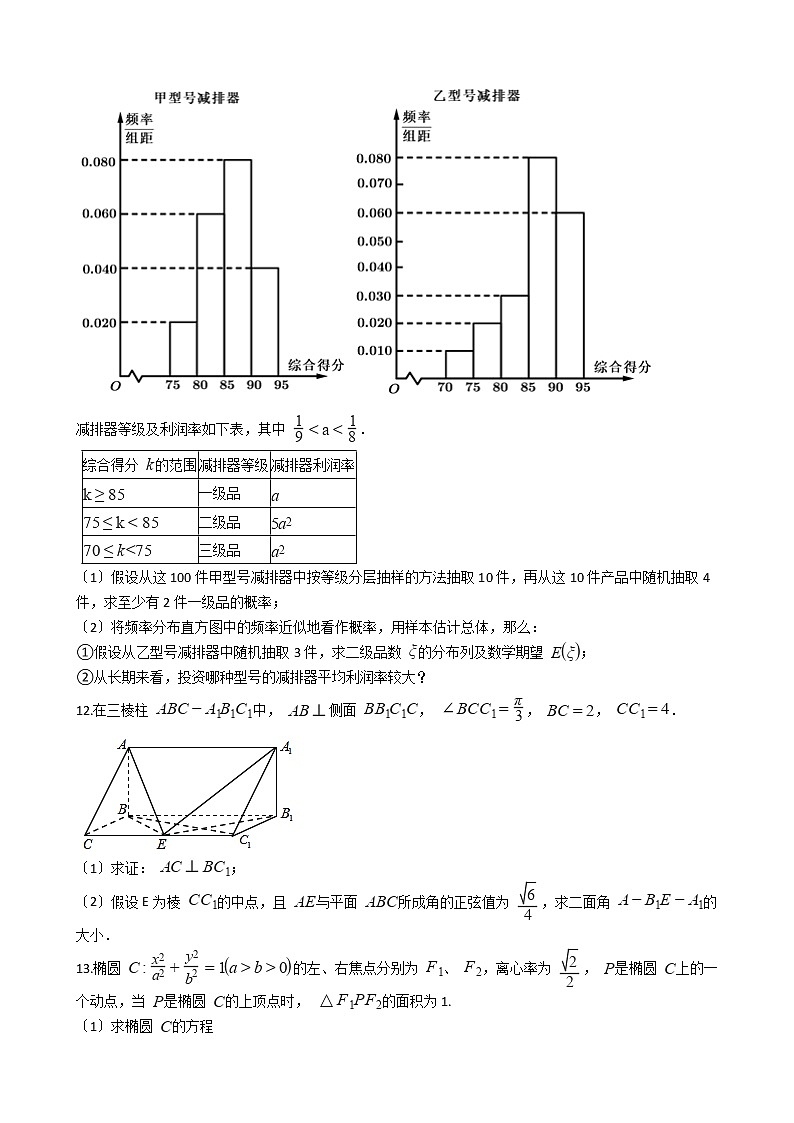
C.                                         D. 二、填空题7.为迎接2022年北京冬奥会，短道速滑队组织甲､乙､丙等6名队员参加选拔赛，比赛结果没有并列名次.记“甲得第一名〞为p，“乙得第一名〞为q，“丙得第一名〞为r，假设 是真命题， 是真命题，那么得第一名的是________.    8.过抛物线 ： 的焦点 的直线与抛物线 交于 ， 两点，假设 ， ，那么 ________．    9.“一湾如月弦初上，半壁澄波镜比明〞描述的是敦煌八景之一的月牙泉.如下列图，月牙泉由两段在同一平面内的圆弧形岸连接围成.两岸连接点间距离为 米.其中外岸为半圆形，内岸圆弧所在圆的半径为60米.某游客绕着月牙泉的岸边步行一周，那么该游客步行的路程为________米.  三、解答题10. 为等差数列，数列 的前 和为 ，___________.在① ，② 这两个条件中任选其中一个，补充在上面的横线上，并完成下面问题的解答(如果选择多个条件分别解答，按第一个解答计分).    〔1〕求数列 和 的通项公式；    〔2〕求数列 的前 项和 .    11.为降低工厂废气排放量，某厂生产甲、乙两种不同型号的减排器，现分别从甲、乙两种减排器中各自抽取100件进行性能质量评估检测，综合得分情况的频率分布直方图如下列图：  减排器等级及利润率如下表，其中 ．综合得分 的范围减排器等级减排器利润率一级品二级品三级品〔1〕假设从这100件甲型号减排器中按等级分层抽样的方法抽取10件，再从这10件产品中随机抽取4件，求至少有2件一级品的概率；    〔2〕将频率分布直方图中的频率近似地看作概率，用样本估计总体，那么：  ①假设从乙型号减排器中随机抽取3件，求二级品数 的分布列及数学期望 ；②从长期来看，投资哪种型号的减排器平均利润率较大？12.在三棱柱 中， 侧面 ， ， ， ．  〔1〕求证： ；    〔2〕假设E为棱 的中点，且 与平面 所成角的正弦值为 ，求二面角 的大小．    13.椭圆 的左、右焦点分别为 、 ，离心率为 ， 是椭圆 上的一个动点，当 是椭圆 的上顶点时， 的面积为1.    〔1〕求椭圆 的方程    〔2〕设斜率存在的直线 ，与椭圆 的另一个交点为 .假设存在 ，使得 ，求 的取值范围    14.设函数 .    〔1〕假设 的图象的一条切线 在 轴上的截距为1，求切线 的方程；    〔2〕求函数 的极值点个数.    15.曲线 的极坐标方程为 ，以极点为平面直角坐标系的原点，极轴为 的正半轴，建立平面直角坐标系 . 〔1〕假设曲线 为参数〕与曲线 相交于两点 ，求 ；    〔2〕假设 是曲线 上的动点，且点 的直角坐标为 ，求 的最大值.    16.设函数 ．    〔1〕求 的最小值 ；    〔2〕在〔1〕的件下，证明 ．   
答案解析局部一、单项选择题1.【解析】【解答】集合 ，且 有16个子集， 那么 有4个元素，由 ，由元素的互异性可得 .故答案为：A 
【分析】由 有16个子集，得有4个元素，再由元素的互异性可得a的值。2.【解析】【解答】由 即复数 ，所以复数对应的点为 位于第二象限.故答案为：B【分析】根据三角函数的诱导公式，求得复数 ，结合复数的几何意义，即可求解.3.【解析】【解答】对A，由图象可得，第3天至第10天两名运发动综合得分均超过80分，A正确，不符合题意； 对B，由图象可得，第1天至第7天B运发动的得分逐日提高，B正确，不符合题意；对C，第2天至第3天A运发动的得分增量大于2，B运发动的得分增量小于2，C正确，不符合题意；对D，由图象可得，在第1天至第3天的得分中，A运发动的最小得分78，最高得分80，在第2天至第4天的得分中，最小得分78，最高得分高于80,所以A运发动第1天至第3天的得分方差小于第2天至第4天的得分的方差，D错误，符合题意.综上，错误的结论是D选项.故答案为：D. 
【分析】根据图像，逐项进行分析，即可得出答案。4.【解析】【解答】由题意可知圆心 ，半径为 ，又因为渐近线与圆相交所得弦长为2，那么圆心到渐近线的距离等于 ，双曲线的一条渐近线为 ，运用点到直线的距离公式计算有 ，即 ，所以 ，故 . 故答案为：A. 
【分析】 直接根据圆的弦长公式求出圆心到渐近线的距离，从而建立关于a,b,c的方程，化简即可求得离心率．5.【解析】【解答】作出平面区域如图阴影局部，如图易知，面积为 故旋转一周体积为： 故答案为：B 
【分析】如下列图三角形旋转一周，体积为大圆锥减去小圆锥体积。6.【解析】【解答】函数 〔 且 〕是偶函数，排除B； 当 时， ，可得： ，令 ，作出 与 图像如图：可知两个函数有一个交点，就是函数的一个极值点， ，排除C；当 时， ，故 时，函数 单调递增，时，函数 单调递减，排除A故答案为：D【分析】利用函数的奇偶性排除选项，通过函数的导数求解函数极值点的个数，求出 的值，推出结果即可.二、填空题7.【解析】【解答】由 是真命题，可知p，q中至少有一个是真命题， 又比赛结果没有并列名次，说明第一名要么是甲，要么是乙，那么r是假命题，又 是真命题，那么 是真命题，即p为假命题，故得第一名的是乙，故答案为：乙． 
【分析】分别讨论p,q,r是真命题，然后验证 是真命题， 是真命题是否成立即可。8.【解析】【解答】设 ， 两点的坐标分别为 ， ，显然直线 的斜率存在， 设直线 的方程为 ，联立方程 ，消去 后整理为 ，有 ，又由 ， ，有 ，可得 ，有 ，解得 ．故答案为：4. 
【分析】根据题意画出图形，结合图形设出点A、B的坐标，利用焦点弦公式表示|AF|、|BF|, 列方程组求出p的值.9.【解析】【解答】如图，是月牙湖的示意图， 是 的中点， 连结 ，可得 ，由条件可知 ， 所以 ，所以 ， ，所以月牙泉的周长 .故答案为：  
【分析】连结 ，可得 ，由题意可得 ，可求， ，进而由图利用扇形的弧长公式即可计算得出答案。三、解答题10.【解析】【分析】选 ① 〔1〕由等差数列的根本量法求出公差d后可得通项公式an  ， 再利用 确定数列 是等比数列，从而得出通项公式 ；
〔2〕用分组〔并项〕求和法求和；
选 ② 〔1〕由等差数列的根本量法求出公差d后可得通项公式an  ， 由   求得， 并确定其是等比数列；
〔2〕 用分组〔并项〕求和法求和。11.【解析】【分析】 (1)先根据频率分布直方图分析相应的数据，从而确定甲型号减排器中抽取的样本中各等级减排器的数量，然后利用古典概型的概率计算公式求解所求事件的概率；
(2)①首先确定二级品数ξ所有可能的取值及其相应的概率，列出分布列，并求数学期望E(ξ)；②分别求出甲、乙两型号减排器的利润率的平均值，然后进行比较即可.12.【解析】【分析】〔1〕利用边长关系、勾股定理证明    ，  结合  侧面   ，建立空间直角坐标系证明   即证结论；
〔2〕先利用平面  的法向量 与  成角的余弦值的绝对值等于 ， 解出AB长度，再利用平面 与平面  的法向量所成的角求二面角的大小即可。13.【解析】【分析】〔1〕 由题可知椭圆离心率    ， 当  为椭圆  的上顶点时，  的面积为1 ，列出方程组求解即可得出椭圆  的方程；
〔2〕 设    ，     ， 线段PQ的中点为    ， 直线  的斜率为k，由〔1〕设直线PQ的方程为  ，当  时，  符合题意； 当  时，把  代入    ， 得    ，  利用韦达定理得出   ，由 直线  为线段  的垂直平分线， 得出   ，即 ， 利用根本不等式即可求出  的取值范围 。14.【解析】【分析】〔1〕对函数求导， 设切点坐标为    ， 那么    ，  再由   的图象的一条切线  在  轴上的截距为1 ，即可求出切线  的方程；
〔2〕 由题可知 ，对函数求导，然后设    ， 那么    ，  设    ， 那么 ，再根据导数的正负号判断出单调性即可求出函数  的极值点个数 。   15.【解析】【分析】  在曲线  上，设 ，可得  ， 令 ，那么  ，代入化简即可得出。16.【解析】【分析】〔1〕将  化为分段函数，进而得出 当  时取得最小值； 〔2〕   ，分 及  讨论即可。