2021届上海市浦东新区高三数学三模试卷及答案

 高三数学三模试卷

一、填空题

1.函数 的单调递减区间为________.   

2. ， ，且 ，那么 ________.   

3. ，那么 ________.   

4.假设从总体中随机抽取的样本为：-2､-2､-1､1､1､3､2､2､4､2，那么该总体标准差的点估计值是________.(精确到0.1)   

5.方程 的解是________.   

6.在5张卡片上分别写上数字1、2、3、4、5，然后把它们混合，再任意排成一行组成5位数，那么得到能被2整除的5位数的概率为________.   

7.数列 的前 项和为 ，假设点 〔 〕在函数 的反函数的图像上，那么 =________.   

8.假设复数 ( ， 为虚数单位)满足 ，那么 在复平面上所对应的图形的面积是________.   

x+4y+m=0与圆 〔θ为参数〕没有公共点，那么实数m的取值范围是________．   

10.设函数 的零点为 ､ ､ ，假设 ､ ､ 成等比数列，那么实数 的值为________.   

11.函数 ，假设存在实数 ，使得对于任意的实数x都有 成立，那么实数a的取值范围是________.   

12. ，假设存在 ，使得 与 夹角为 ，且 ，那么 的最小值为________.   

二、单项选择题

13.以下命题正确的选项是〔   〕           

A. 三点确定一个平面
B. 三条相交直线确定一个平面
C. 对于直线a、b、c，假设 ，那么
D. 对于直线a、b、c，假设 ，那么

14.关于x、y的二元一次方程组 的系数行列式 是该方程组有解的〔   〕．           

A. 充分非必要条件          B. 必要非充分条件          C. 充分且必要条件          D. 既非充分也非必要条件

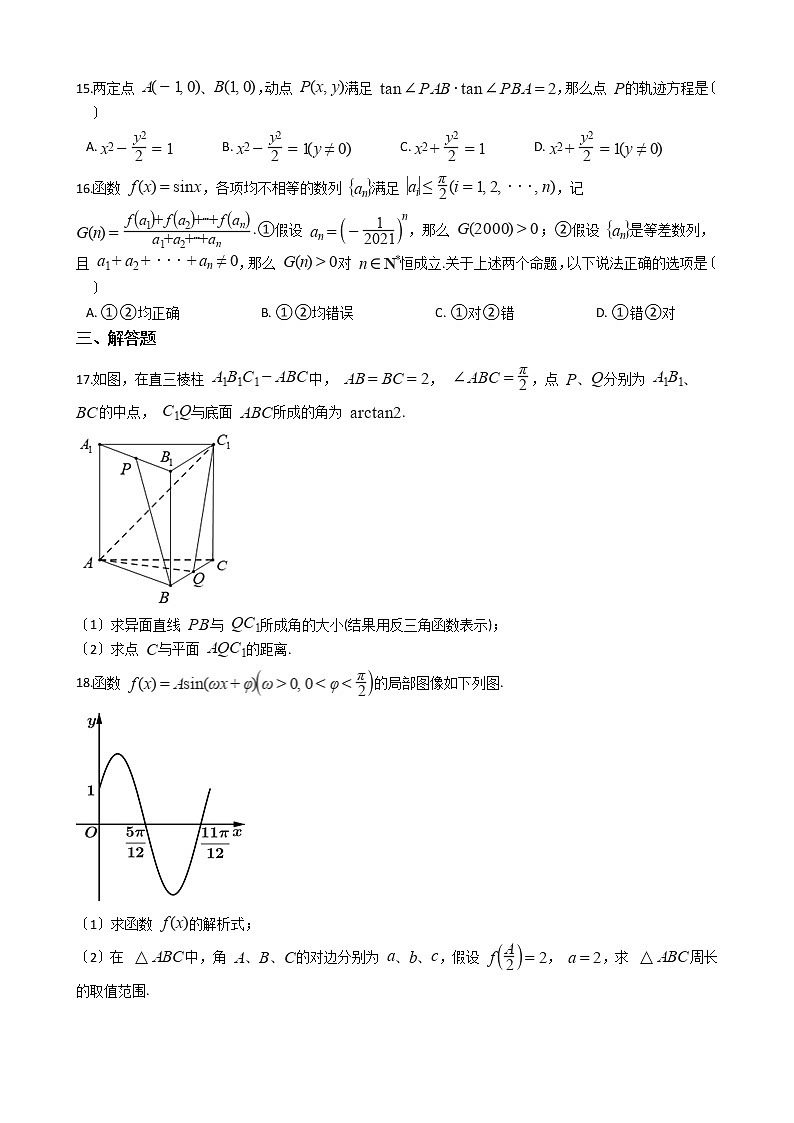
15.两定点 ､ ，动点 满足 ，那么点 的轨迹方程是〔    〕           

A.                B.                C.                D. 

16.函数 ，各项均不相等的数列 满足 ，记 .①假设 ，那么 ；②假设 是等差数列，且 ，那么 对 恒成立.关于上述两个命题，以下说法正确的选项是〔    〕           

A. ①②均正确                         B. ①②均错误                         C. ①对②错                         D. ①错②对

三、解答题

17.如图，在直三棱柱 中， ， ，点 ､ 分别为 ､ 的中点， 与底面 所成的角为 . 

〔1〕求异面直线 与 所成角的大小(结果用反三角函数表示)；   

〔2〕求点 与平面 的距离.   

18.函数 的局部图像如下列图. 

〔1〕求函数 的解析式；   

〔2〕在 中，角 ､ ､ 的对边分别为 ､ ､ ，假设 ， ，求 周长的取值范围.   

19.流行性感冒是由流感病毒引起的急性呼吸道传染病.某市去年11月份曾发生流感，据统计，11月1日该市的新感染者有30人，以后每天的新感染者比前一天的新感染者增加50人.由于该市医疗部门采取措施，使该种病毒的传播得到控制，从11月 日起每天的新感染者比前一天的新感染者减少20人.   

〔1〕假设 ，求11月1日至11月10日新感染者总人数；   

〔2〕假设到11月30日止，该市在这30天内的新感染者总人数为11940人，问11月几日，该市新感染者人数最多？并求这一天的新感染者人数.   

20.直线 与椭圆 交于 、 两点〔如下列图〕，且 在直线l的上方. 

〔1〕求常数t的取值范围；   

〔2〕假设直线 、 的斜率分别为 、 ，求 的值；   

〔3〕假设 的面积最大，求 的大小.   

21. ， 为两非零有理数列〔即对任意的 ， ， 均为有理数〕， 为一无理数列〔即对任意的 ， 为无理数〕.   

〔1〕 ，并且 对任意的 恒成立，试求 的通项公式.   

〔2〕假设 为有理数列，试证明：对任意的 ， 恒成立的充要条件为 .   

〔3〕 ， ，对任意的 ， 恒成立，试计算 .   

答案解析局部

一、填空题

1.【解析】【解答】令 ，那么 ，

∵ 在 单调递减， 在 单调递增，

根据复合函数的单调性可得： 在 单调递减，

故答案为： .

 
【分析】求得函数的定义域，由复合函数的单调性，即可得到单调区间。

2.【解析】【解答】∵ ，∴ .

故答案为：6.

 
【分析】由两个向量共线的性质可得， 解方程可得x的值。

3.【解析】【解答】 .

故答案为： .

 
【分析】 利用二阶行列式，展开 利用三角函数的同角公式化成关于cosx的形式，根据 求解即可.

4.【解析】【解答】解：由，样本的平均值为 ，

所以样本标准差的点估计值为

，

所以总体标准差的点估计值是1.9，

故答案为：1.9.

 
【分析】 先求出偶样本数据的平均数，然后总体标准差的点估计值的求解公式计算即可.

5.【解析】【解答】解：因为

 
【分析】由条件可得， 求解即可得出。

6.【解析】【解答】能被2整除的5位数的个位数为2或4，所以，能被2整除的5位数的个数为 ，

因此，所求概率为 .

故答案为： .

 
【分析】 确定组成5位数的个数，五位数能被2整除的特征及个数，利用概率公式，即可得到结论.

7.【解析】【解答】解：因为

 
【分析】 先利用点  都在f(x)的反函数图象上即点(Sn,n)都在f(x)的原函数图象上，得到关于Sn的表达式；再利用前n项和为Sn求数列{an }的通项公式的方法即可求数列{an}的通项公式。

8.【解析】【解答】复数 在复平面内对应的点为 ，而满足 所表示的区域如以下列图所示：

由上图可知 在复平面上所对应的图形的面积为 .

故答案为：2.

 
【分析】 利用复数的几何意义结合|x|+ |y|≤1,得到z在复平面上所对应的图形，然后求解面积可得到答案.

9.【解析】【解答】此圆的圆心为(1.-2)，因为要没有公共点，所以根据圆心到直线的距离大于半径即可

得： 解得 或 ．

 
【分析】 直接利用圆的参数方程的应用和点到直线的距离公式的应用求出结果.

10.【解析】【解答】解：原问题等价于 与 有三个不同的交点，且交点的横坐标分别为 ､ ､ ，结合余弦函数图象，由对称性得， ， ，

又 ，

∴ ，

∴ ，

∴ ，

故答案为： .

 
【分析】 由题意得x2 = 2π-x1, x3= 2π+x1,然后结合等比数列的性质可求x1,进而可求m.

11.【解析】【解答】分别作出 、 的图象中以下列图所示，

由图可以看出当 时， 有确定的最大值 ，所以这时存在 ，使得对于任意x都有 .

故答案为： .

 
【分析】画出分段函数的图像，根据图像可得出实数a的取值范围 。

12.【解析】【解答】由题意， ，

∴令 ， ，故有 共线，

∵ ，故当且仅当 为最小时， 最小，

∴有 、 关于y轴对称时， 最小，此时 到AB的距离为 ，

∴ ，即 .

故答案为： .

 
【分析】 由题意画出图形，令 ，， 可得A, A', B, B'共线，进一步说明当A'、B'关于y轴对称时，| AB|最小，求出O到AB的距离，进一步求得|AB|的最小值.

二、单项选择题

13.【解析】【解答】解:A.不共线的 三点确定一个平面；

B. 三条相交直线确定一个平面或者两个，或者三个平面，；

C. 对于直线a、b、c，假设 ，那么 ，可能相交也可能异面，错误

D. 对于直线a、b、c，假设 ，那么 ，利用平行传递性成立．

故答案为：D

 
【分析】 不共线的三点确定一个平面，A错误;三条相交直线可确定一个平面，或三个平面，(三棱锥的三条侧棱)，B错误; ，那么 ， 在立体几何中不一定成立，C错误;选项D，由平行公理可得答案。

14.【解析】【解答】此题选D。因为系数行列式D不为零时，方程组有唯一解，说明条件不必要；
当系数行列式D为零时，方程组可能有无数个解或无解，故条件也不充分.
故答案为：D。
【分析】注意系数行列式为零和不为零时，方程组解的情况。

15.【解析】【解答】 ， ，

∴ ，

故答案为：D.

 
【分析】 由题意得， 化简可得结果。

16.【解析】【解答】解： 在 为奇函数且单调递增，

①

所以 ，且 ，①正确；

② 是等差数列，当 时，

假设 为偶数， ，

，

同理 ，…， ，

所以

假设 为奇数， ，

， ，…，

所以 ；

同理，当 时，也有 .②正确.

故答案为：A

 
【分析】 先分析出 在 上为奇函数且单调递增，再根据函数的性质以及等差数列的性质逐个分析①②即可求解.

三、解答题

17.【解析】【分析】〔1〕建立空间直角坐标系，将问题转化为  与  的夹角即可求解；

〔2〕求出平面  的法向量 ， 利用点   与平面  的距离为 即可求解。

18.【解析】【分析】〔1〕 由题意求出A，T，利用周期公式求出ω，把点代入，求出φ，得到函数 的解析式；
〔2〕 由  ，  ， ， 再由 正弦定理 得

，   ，进而得出 周长的取值范围.

19.【解析】【分析】 (1) 记11月n日新感染者人数为    ， 然后利用数列  是等差数列 ，
由等差数列前n项求和公式求解即可;
(2)由题意，分别求出当1≤n≤k，k+1≤n≤30时的an,然后利用等差数列前n项求和公式，求出k的值，即可得到答案.

20.【解析】【分析】 (1)由  在直线l的上方可得t < 0联立直线l与椭圆方程，由△> 0可得t2 < 8,从而求出t的取值范围；
(2) 设  、  ， 由韦达定理可得   ，  ，代入  化简即可求出 ；
(3)由弦长公式求出|AB|，再利用点到直线距离公式求出点P到直线AB的距离d,代入 ,再结合根本不等式，即可求出△APB的面积最大时∠APB的大小.

21.【解析】【分析】 (1)由   可得   由   ，可得   , 解出即可得出  的通项公式 ；
(2)由   ， 可得 ，利用  为有理数列，即可证明；
(3)由体积可得  分类讨论，利用{an}, {bn}, {dn3}为有理数列，{dn}为无理数列，即可得出.