2020-2021年河南省郑州市九年级上学期数学10月月考试卷及答案

这是一份2020-2021年河南省郑州市九年级上学期数学10月月考试卷及答案，共11页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
 九年级上学期数学10月月考试卷
一、单项选择题
1.以下条件中，能判断四边形是菱形的是〔   〕
A. 对角线互相垂直且相等的四边形                         B. 对角线互相垂直的四边形
C. 对角线相等的平行四边形                                    D. 对角线互相平分且垂直的四边形
〔x+1〕＝3x+2化为一般形式，正确的选项是〔    〕
A. x2+4x+3＝0                  B. x2﹣2x+2＝0                  C. x2﹣3x﹣1＝0                  D. x2﹣2x﹣2＝0
3.假设a、b是关于x的一元二次方程x2﹣6x+n+1=0的两根，且等腰三角形三边长分别为a、b、4，那么n的值为〔   〕
A. 8                                        B. 7                                        C. 8或7                                        D. 9或8
4.一个盒子中装有标号为1，2，3，4，5，的五个小球，这些球除标号外都相同，从中随机摸出两个小球，那么摸出的小球标号之和大于5的概率为〔     〕
A.                                           B.                                           C.                                           D. 
5.为执行“均衡教育“政策，某区2021年投入教育经费2500万元，预计到2021年底三年累计投入1.2亿元，假设每年投入教育经费的年平均增长百分率为x，那么以下方程正确的选项是(     )
A. 2500(1+2x)=12000                                           B. 2500+2500(1+x)+2500(1+2x)=12000
C. 2500(1+x)2=1200                                             D. 2500+2500(1+x)+2500(1+x)2=12000
6.以下数中，能与6，9，10组成比例的数是〔   〕
A. 1                                         B. 74                                         C. 5.4                                         
7.如图，菱形ABCD的两条对角线AC，BD相交于点O，E是AB的中点，假设AC＝6，菱形ABCD的面积为24，那么OE长为〔   〕

A. 2.5                                          B. 3.5                                          C. 3                                          D. 4
8.如图,矩形ABCD,点E. F分别在AD、BC上且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,假设AB= ，那么CG为〔   〕

A. 3.                                         B. 1.                                         C. 2.                                         D. .
二、填空题
9. ，那么 ________.
10.如以下列图，长为8cm，宽为6cm的矩形中，截去一个矩形〔图中阴影局部〕，如果剩下矩形与原矩形相似，那么剩下矩形的面积是 ________

11.假设(m-1) +2mx-1=0是关于x的一元二次方程，那么m的值是________.
12.在一个不透明的袋子中装有20个蓝色小球、假设干个红色小球和10个黄色小球，这些球除颜色不同外其余均相同，小李通过屡次摸取小球试验后发现，摸取到红色小球的频率稳定在0.4左右，假设小明在袋子中随机摸取一个小球，那么摸到黄色小球的概率为 ________
13.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,那么DE的长度为________.

14.如图，菱形ABCD的边长为4，∠B＝120°.点P是对角线AC上一点〔不与端点A重合〕，那么线段 AP+PD的最小值为________.

15.矩形纸片ABCD，AB=9，BC=6，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E，F，那么EF长为________．
三、解答题
以下方程：
〔1〕
〔2〕
17.某商场在促销活动中规定，顾客每消费100元就能获得一次抽奖时机.为了活泼气氛，设计了两个抽奖方案：
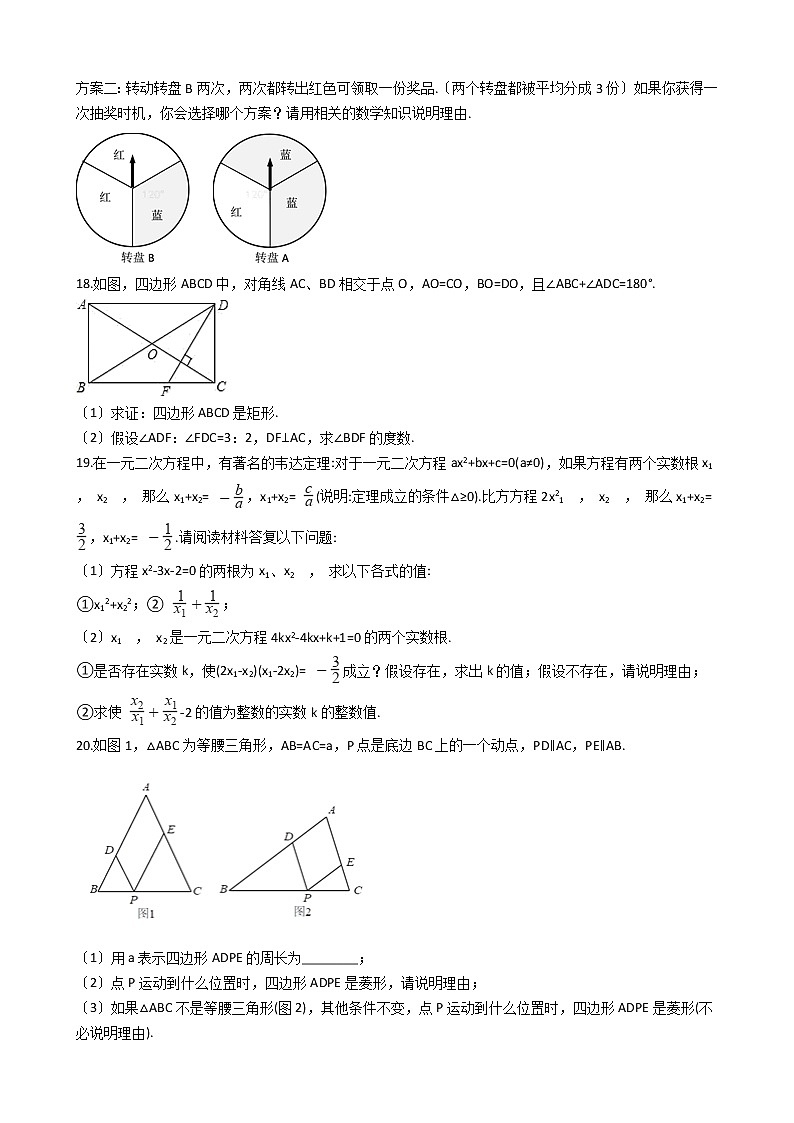
方案一：转动转盘A一次，转出红色可领取一份奖品；
方案二：转动转盘B两次，两次都转出红色可领取一份奖品.〔两个转盘都被平均分成3份〕如果你获得一次抽奖时机，你会选择哪个方案？请用相关的数学知识说明理由.
   
18.如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°.

〔1〕求证：四边形ABCD是矩形.
〔2〕假设∠ADF：∠FDC=3：2，DF⊥AC，求∠BDF的度数.
19.在一元二次方程中，有著名的韦达定理:对于一元二次方程ax2+bx+c=0(a≠0)，如果方程有两个实数根x1 ， x2 ， 那么x1+x2= ，x1+x2= (说明:定理成立的条件△≥0).比方方程2x21 ， x2 ， 那么x1+x2= ，x1+x2= .请阅读材料答复以下问题:
〔1〕方程x2-3x-2=0的两根为x1、x2 ， 求以下各式的值:
①x12+x22；② ；
〔2〕x1 ， x2是一元二次方程4kx2-4kx+k+1=0的两个实数根.
①是否存在实数k，使(2x1-x2)(x1-2x2)= 成立？假设存在，求出k的值；假设不存在，请说明理由；
②求使 -2的值为整数的实数k的整数值.
20.如图1，△ABC为等腰三角形，AB=AC=a，P点是底边BC上的一个动点，PD∥AC，PE∥AB.

〔1〕用a表示四边形ADPE的周长为________；
〔2〕点P运动到什么位置时，四边形ADPE是菱形，请说明理由；
〔3〕如果△ABC不是等腰三角形(图2)，其他条件不变，点P运动到什么位置时，四边形ADPE是菱形(不必说明理由).
2021年从网上购置 张电影票的费用比现场购置 张电影票的费用少 元:从网上购置 张电影票的费用和现场购置 张电影票的费用共 元.
〔1〕求该电影城2021年在网上购票和现场购票每张电影票的价格为多少元?
〔2〕2021年五一当天，该电影城按照2021年网上购票和现场购票的价格销售电影票，当天售出的总票数为 张.五一假期过后，观影人数出现下降，于是电影城决定从5月5日开始调整票价：现场购票价格下调，网上购票价格不变，结果发现，现场购票每张电影票的价格每降低 元，售出总票数就比五一当天增加 张.经统计，5月5日售出的总票数中有 的电影票通过网上售出，其余通过现场售出，且当天票房总收入为 元，试求出5月5日当天现场购票每张电影票的价格为多少元?
22.如图1，平面直角坐标系中，B、C两点的坐标分别为B〔0，3〕和C〔0，﹣ 〕，点A在x轴正半轴上，且满足∠BAO＝30°.

〔1〕过点C作CE⊥AB于点E，交AO于点F，点G为线段OC上一动点，连接GF，将△OFG沿FG翻折使点O落在平面内的点O′处，连接O′C，求线段OF的长以及线段O′C的最小值；
〔2〕如图2，点D的坐标为D〔﹣1，0〕，将△BDC绕点B顺时针旋转，使得BC⊥AB于点B，将旋转后的△BDC沿直线AB平移，平移中的△BDC记为△B′D′C′，设直线B′C′与x轴交于点M，N为平面内任意一点，当以B′、D′、M、N为顶点的四边形是菱形时，求点M的坐标.

答案解析局部
一、单项选择题
1.【解析】【解答】解：A、对角线互相垂直相等的四边形不一定是菱形，此选项错误；
B、对角线互相垂直的四边形不一定是菱形，此选项错误；
C、对角线相等的平行四边形也可能是矩形，此选项错误；
D、对角线互相平分且垂直的四边形是菱形，此选项正确；
故答案为：D.
【分析】利用菱形的判定定理，对各选项逐一判断，可得答案。
2.【解析】【解答】解：去括号得：x2+x＝3x+2
移项合并得：x2﹣2x﹣2＝0
故答案为：D
【分析】先去括号，再移项，然后合并同类项，即可得出答案。
3.【解析】【解答】解：∵等腰三角形三边长分别为a、b、4，
∴a=b，或a、b中有一个数为4．
当a=b时，有b2﹣4ac=〔﹣6〕2﹣4〔n+1〕=0，
解得：n=8；
当a、b中有一个数为4时，有42﹣6×4+n+1=0，
解得：n=7，
应选C．
【分析】由等腰三角形的性质可知“a=b，或a、b中有一个数为4〞，当a=b时，由根的判别式b2﹣4ac=0即可得出关于k的一元一次方程，解方程可求出此时n的值；a、b中有一个数为4时，将x=4代入到原方程可得出关于n的一元一次方程，解方程即可求出此时的n值，结合三角形的三边关系即可得出结论．
4.【解析】【解答】解：根据题意可得树状图为：

一共有25种结果，其中15种结果是大于5的
因此可得摸出的小球标号之和大于5的概率为
故答案为：C.

【分析】根据树状图可得一共有25种结果，小球标号之和大于5的结果有15种，从而得到所求概率。
5.【解析】【解答】解：设每年投入教育经费的年平均增长百分率为x，
由题意得, 2500+2500(1+x)+2500(1+x)2=12000
故答案为：D.
【分析】由题意可知等量关系为： 2021年投入教育经费+2021年投入教育经费+2021年投入教育经费=1200，列方程即可。
6.【解析】【解答】解：A、10×1≠6×9，1不能与6，9，10组成比例，故错误；
B、6×74≠9×10，74不能与6，9，10组成比例，故错误；
C、5.4×10＝6×9，5.4能与6，9，10组成比例；故正确；
D、1.5×10≠6×9，1.5不能与6，9，10组成比例，故错误.
故答案为：C.
【分析】利用比例的性质：两内项之积等于两外项之积，即可作出判断。
7.【解析】【解答】解：∵四边形ABCD是菱形，AC＝6，菱形ABCD的面积为24，
∴ ，
解得：BD＝8，
∴AO＝OC＝3，OB＝OD＝4，AO⊥BO，
又∵点E是AB中点，
∴OE是△DAB的中线，
在Rt△AOD中，AB= ＝5，
那么OE＝ AD＝2.5.
故答案为：A.
【分析】利用菱形的面积等于两对角线之积的一半，就可求出BD的长，再利用菱形的对角线互相垂直平分，可求出OA，OD的长，利用勾股定理求出AB的长；然后根据直角三角形斜边上的中线等于斜边的一半，就可求出OE的长。
8.【解析】【解答】解：连接AF,如以下列图,

∵四边形ABCD为矩形，
∴AD∥BC，AD=BC，
∴∠AEF=∠GFE.
由折叠的性质可知：AB=HG,BF=HF,∠ABF=∠GHF=90°，∠BFE=∠HFE，
∴△ABF≌△GHF,
∴AF=FG，∠AFB=∠GFH，
∴∠AFE=∠GFE，
∴∠AEF=∠AFE，
∴AF=AE.
设BF=2x，那么AD=BC=6x，AF=AE=FG=3x，CG=BC−BF−FG=x.
在Rt△ABF中,∠B=90°,AB= ，AF=3x，BF=2x，
∴AF2=AB2+BF2,即(3x)2=(2x)2+( )2 ，
解得：x=1或x=−1(舍去)，
∴CG=x=1.
故答案为：B.
【分析】连接AF，利用矩形的性质，易证AD∥BC，AD=BC，可推出∠AEF=∠GFE，再利用折叠的性质AB=HG,BF=HF,∠ABF=∠GHF=90°，∠BFE=∠HFE，从而可证得△ABF≌△GHF，利用全等三角形的性质，可得到AF=FG，∠AFB=∠GFH，再去证明AF=AE，设BF=2x，用含x的代数式AF，BF，然后利用勾股定理建立关于x的方程，解方程求出x的值，即可得到CG的长。
二、填空题
9.【解析】【解答】解： ，
设 ， ，
.
故答案为： .
【分析】利用a与b的比值，设a=2k，b=3k，再将a，b分别代入代数式，然后化简可求值。
10.【解析】【解答】解：依题意，在矩形ABDC中截取矩形ABFE，

那么矩形ABDC∽矩形FDCE，
那么
设DF＝xcm，得到： ，
解得：x＝4.5，
那么剩下的矩形面积是：4.5×6＝27cm2.
故答案为：27cm2
【分析】利用四边形相似的性质，可得到对应边成比例，建立关于x的方程，解方程求出x的值，然后求出剩下的矩形的面积。
11.【解析】【解答】解：由题意，得
m〔m+2〕-1=2且m-1≠0，
解得m=-3，
故答案为：-3.
【分析】含有一个未知数，未知数的最高次数是二次，二次项的系数不为0的整式方程就是一元二次方程，根据定义即可列出混合组，求解即可。
12.【解析】【解答】解：设袋子中红球有x个，
根据题意,得： =0.4，
解得：x=20，
经检验：x=20是原分式方程的解，
那么小明在袋子中随机摸取一个小球,摸到黄色小球的概率为= ，
故答案为： .
【分析】设袋子中红球有x个，由题意可知红色小球的概率为0.4，据此建立方程求出x的值，然后利用概率公式可求出摸到黄色小球的概率。
13.【解析】【解答】解：由题意可得出：∠BDC=45°,∠DA′E=90°，
∴∠DEA′=45°，
∴A′D=A′E，
∵在正方形ABCD中，AD=1，
∴AB=A′B=1，
∴BD= ，
∴A′D= −1，
∴在Rt△DA′E中,DE= =2− .
故答案为：2− .
【分析】利用正方形的性质和旋转的性质，可知∠BDC=45°，∠DA′E=90°，由此可证得A′D=A′E，再利用勾股定理求出BD的长，就可求出A′D，在Rt△DA′E中，利用解直角三角形求出DE的长。
14.【解析】【解答】解：如图，作PE⊥AB于点E，DF⊥AB于点F，

∵四边形ABCD是菱形
∴∠DAC=∠CAB，AB=BC，且∠B=120°
∴∠CAB=30°
∴PE= AP，∠DAF=60°
∴∠FDA=30°，且DF⊥AB
∴AF= AD=2，DF= AF=2
∵ AP+PD=PE+DP
∴当点D，点P，点E三点共线且垂直AB时，PE+DP的值最小，最小值为DF，
∴线段 AP+PD的最小值为2
故答案为：2
【分析】作PE⊥AB于点E，DF⊥AB于点F，利用菱形的性质，可得到∠DAC=∠CAB，AB=BC，∠B=120°，可推出∠CAB=30°，再利用直角三角形的性质，可得到PE= AP，AF= AD，从而可求出AF，DF的长，然后利用两点之间线段最短，可知当点D，点P，点E三点共线且垂直AB时，PE+DP的值最小，最小值为DF，即可求解。
15.【解析】【解答】解：如图1，当点P在CD上时，


∵PD=3，CD=AB=9，
∴CP=6，∵EF垂直平分PB，
∴四边形PFBE是正方形，EF过点C，
∴EF=6 ，
如图2，当点P在AD上时，

过E作EQ⊥AB于Q，
∵PD=3，AD=6，
∴AP=3，
∴PB= = =3 ，
∵EF垂直平分PB，
∴∠1=∠2，
∵∠A=∠EQF，
∴△ABP∽△EFQ，
∴ ，
∴ ，
∴EF=2 ，
综上所述：EF长为6 或2 ．
故答案为：6 或2 ．
【分析】如图1，当点P在CD上时，由折叠的性质得到四边形PFBE是正方形，EF过点C，根据勾股定理即可得到结果；如图2当点P在AD上时，过E作EQ⊥AB于Q，根据勾股定理得到PB= = =3 ，推出△ABP∽△EFQ，列比例式即可得到结果．
三、解答题
16.【解析】【分析】〔1〕将一元二次方程转化为一般形式，观察可得方程的左边可以分解因式，因此利用因式分解法解方程。
〔2〕观察方程左右两边的特点：右边可以分解因式，方程两边都含有公因式〔x-2〕，因此利用因式分解法解方程。
17.【解析】【分析】由题意可直接得到方案一获得奖品的概率；再利用列表求出方案二的概率，然后比较大小，可得到结果。
18.【解析】【分析】〔1〕利用对角线互相平分的四边形是平行四边形，可证四边形ABCD是平行四边形；再利用平行四边形的对角相等及∠ABC+∠ADC=180°，就可求出∠ABC=90°，然后利用有一个角是直角的平行四边形是矩形，可证得结论。
〔2〕由∠ADC=90°及∠ADF：∠FDC=3：2，求出∠FDC的度数，再利用直角三角形的两锐角互余，求出∠DCO的度数，然后根据矩形的性质及等边对等角，可求出∩ODC的度数根据∠BDF=∠ODC-∠FDC，从而可求出∠BDF的度数。
19.【解析】【分析】〔1〕①利用韦达定理可求出 x1+x2和x1•x2的值， 再利用配方法将x12+x22转化为 (x1+x2)2-2x1•x2 ， 然后整体代入即可；②先通分，将代数式转化为含x1+x2和x1•x2的形式，然后整体代入可求值。
〔2〕①利用一元二次方程根的判别式求出k的取值范围，再求出x1+x2和x1•x2的值，然后将等式的左边转化为含x1+x2和x1•x2 ， 然后整体代入建立关于k的方程，解方程求出k的值，再根据k的取值范围可作出判断；②先通分将原代数式转化为含x1+x2和x1•x2 ， 然后整体代入可得到关于k的方程，再根据此代数式的值为整数，可得到k+1=±1或±2或±4， 解方程求出符合题意的k的值。
20.【解析】【解答】解：⑴∵PD∥AC，PE∥AB，
∴四边形ADPE为平行四边形，
∴AD=PE，DP=AE，
∵AB=AC，
∴∠B=∠C，
∵DP∥AC，
∴∠B=∠DPB，
∴DB=DP，
∴四边形ADPE的周长=2(AD+DP)=2(AD+BD)=2AB=2a；
故答案为：2a；
【分析】〔1〕根据有两组对边分别平行的四边形是平行四边形，可证得四边形ADPE为平行四边形，利用平行四边形的对边相等，可证得AD=PE，DP=AE，再利用等腰三角形的判定和性质去证明DP=BD，然后可得到四边形ADPE的周长就等于2AB。
〔2〕连接AP，由〔1〕可知四边形ADPE为平行四边形，利用等腰三角形的性质易证∠PAD=∠PAE，利用两直线平行，内错角相等，可证得∠PAD=∠APE，继而可证∠PAE=∠APE，利用等角对等边，可证得EA=EP，然后根据有一组邻边相等的平行四边形是菱形，可证得结论。
〔3〕通过分析可知P运动到∠A的平分线上时，四边形ADPE是菱形， 同理可证四边形ADPE是平行四边形，再证明AE=PE，然后根据有一组邻边相等的平行四边形是菱形，可证得结论。
21.【解析】【分析】〔1〕由题意可知等量关系为：3×网上每张电影票的价格-2×现场每张电影票的价格=-10；5×网上每张电影票的价格+1×现场每张电影票的价格=200，设未知数，列方程组，然后求出方程组的解。
〔2〕抓住关键的条件，根据当天票房总收入=17680，设未知数，列方程，求出符合题意的x的值即可。
22.【解析】【分析】〔1〕根据直角三角形的两锐角互余求出∠CBE的度数，由垂直的定义可求出∠BCE的度数，由点C的坐标求出OC的长，再在Rt△OCF中，利用解直角三角形求出OF的长；然后利用折叠的性质，可得到FO′的长，然后根据CO′≥CF-O′F，可求出线段O′C的最小值。
〔2〕分四种情况讨论： ①如图2中，利用勾股定理求出B′M的长，可得到B′D′=B′M=BD时 ，可得菱形MND′B′.，再求OM的长，就可得点M的坐标；②如图3中，当B′M是菱形的对角线时，由题意可知B′M=2OB=6，再求出AM，OM的长，可得点M的坐标；③如图4中，当B′D′是菱形的对角线时，由∠D′B′M=∠DBO；利用解直角三角形求出B′M、AM、OM的长，从而可求出点M的坐标； ④如图5中，当MD′是菱形的对角线时，可得到MB′=B′D′，再求出AM ，OM的长，然后可得到点M的坐标，综上所述，可得到符合题意的点M的坐标。