初中数学第十四章 整式的乘法与因式分解综合与测试教案设计

这是一份初中数学第十四章 整式的乘法与因式分解综合与测试教案设计，共7页。
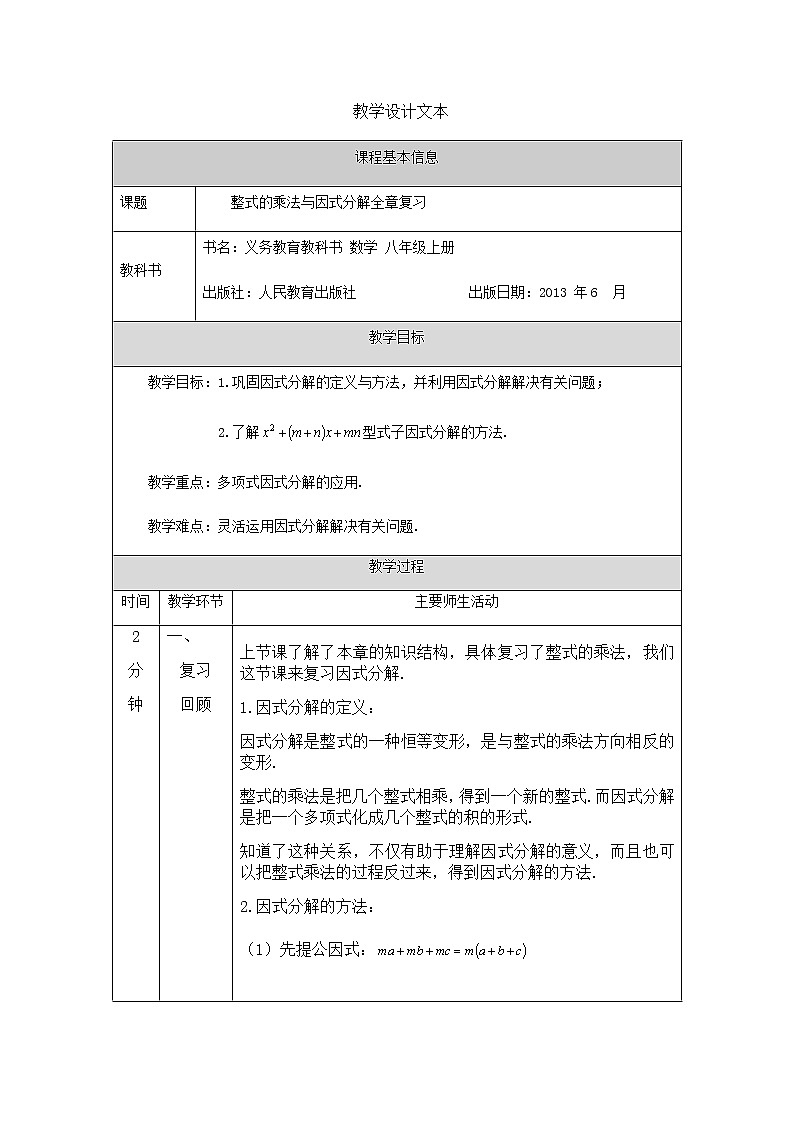
 教学设计文本课程基本信息课题整式的乘法与因式分解全章复习教科书书名：义务教育教科书 数学 八年级上册                                出版社：人民教育出版社                出版日期：2013 年6  月教学目标教学目标：1.巩固因式分解的定义与方法，并利用因式分解解决有关问题；2.了解型式子因式分解的方法.教学重点：多项式因式分解的应用.教学难点：灵活运用因式分解解决有关问题.教学过程时间教学环节主要师生活动2分钟            一、复习回顾              上节课了解了本章的知识结构，具体复习了整式的乘法，我们这节课来复习因式分解.1.因式分解的定义：因式分解是整式的一种恒等变形，是与整式的乘法方向相反的变形.整式的乘法是把几个整式相乘，得到一个新的整式.而因式分解是把一个多项式化成几个整式的积的形式.知道了这种关系，不仅有助于理解因式分解的意义，而且也可以把整式乘法的过程反过来，得到因式分解的方法.2.因式分解的方法：（1）先提公因式：（2）观察项数：（3）检查分解是否彻底.对于完全平方公式中的(a±b)2具有非负性，可以帮助我们解决一些问题.12分钟                                                                               二、典例选讲                                                       例1.下列各式中，从左到右的变形属于因式分解的是（    ）.A.；        B.；    C.；  D..分析：（1）审题：从左到右的变形（2）选项A，等式右边没有化成乘积的形式，它是两个整式相乘，得到了一个新的整式，属于整式的乘法；选项B，等式右边没有化成乘积的形式；选项C，首先从形式上符合因式分解，分解的是否正确呢？，我们不难判断出，选项C是正确的.当然我们也可以利用整式乘法与因式分解是相反的变形，来进行判断；选项D，等式右边出现了分母中含有字母的式子，它不是整式，不属于因式分解.小结1：判断变形是否属于因式分解，这个变形要符合因式分解定义的每一个条件.例2.分解因式：（1）；         （2）.分析：观察代数式的特点，结合因式分解的步骤分析.解：（1）       小结2：分解因式中，提公因式是我们的首选方法，检查因式分解是否彻底也是很关键的一步.     （2）法一：  法二：小结3：通过观察代数式的特点，如果能够直接分解因式，就可以直接分解因式，如果没有观察出来，也可以先整理，然后再分解因式.巩固练习：分解因式（1）；   （2）.解：（1）     （2）                        因式分解作为一种重要的恒等变形，在一些问题的解决中，有着重要的作用.例3.（1）已知，，求的值；（2）若，求的值.（1）分析：观察题目已知中的代数式与，与所求值的代数式之间的关系.解：将代入，原式=.（2）分析：观察题目中的条件，如何确定x，y值？解：         .小结4：通过观察题目中代数式的特征，从比较复杂的条件入手，利用分解因式进行计算，或者化简，从而解决问题.10分钟                                       三、知识拓展探究：分解因式：观察这个代数式发现，提公因式法和公式法都不能将其分解因式，下面一起来探究，某些二次项系数为1的二次三项式如何分解因式.利用整式乘法可以得到：，因式分解与整式乘法是方向相反的变形，，某些二次项系数为1的二次三项式可以分解为两个一次二项式乘积的形式，关键确定m，n的值，下面以为例：         拆： 凑：像这种分解因式的方法叫做十字相乘法.能使用十字相乘法分解因式的式子的特征：（1）三项；（2）二次；（3）二次项系数为1；（4）常数项mn，一次项系数m+n.注意：1.竖拆二次项系数和常数项；2.横写分解因式结果.小结5：型式子因式分解的步骤：1.拆常数项；2.凑一次项；3.横写结果.当然我们在拆凑的过程中，可以先观察常数项与一次项系数的符号.常数项6>0，有四种拆法，分为两类，同正，同负，而一次项系数为5>0，分得的两数的和为正，那么只拆凑同正的情况就可以了.这样可以减少尝试的次数，提高做题的速度.例4.分解因式：   解：拆： 凑： 小结6：先观察符号，再进行拆凑，多次尝试，不断积累经验，会比较迅速地找到正确的结果.巩固练习：分解因式          解：拆：  凑：      十字相乘法也可以分解某些二次项系数不为1的二次三项式，同学们课下可以尝试一下.1分钟      四、归纳总结1.复习因式分解的定义与方法，并利用因式分解解决有关问题；2.了解型式子因式分解的方法.五、课后练习 1.分解因式：（1）       （2）（3）          （4）2.已知，，求的值.