人教版七年级上册3.1.1 一元一次方程课文配套课件ppt

这是一份人教版七年级上册3.1.1 一元一次方程课文配套课件ppt，共17页。PPT课件主要包含了新课引入，2x-2，一元一次方程，小试身手等内容，欢迎下载使用。
判断下列各式是不是方程，是的打“√”，不是的打“ｘ”。 (1) -2+5=3 ( ) (2) 3χ-1=7 ( ) (3) m=0 ( ) (4) χ﹥ 3 ( ) (5) χ+y=8 ( ) (6) 2χ2-5χ+1=0 ( ) (7) 2a +b ( ) （8） = 4 （ ）
含有未知数的等式叫做方程.
2004年夏季奥运会上,我国获得32枚金牌。其中跳水队获得6枚金牌，比射击队获得金牌数的2倍少2枚。射击队获得多少枚金牌？
如果设射击队获得的金牌数为x
奥运冠军朱启南在雅典奥运会男子10米气步枪决赛中最后两枪的平均成绩为10.4环，其中第10枪(最后一枪)的成绩为10.1环,问第9枪的成绩是多少环？
设第9枪的成绩为x环,可列出方程: 。
人教版七年级上册3.1 从算式到方程 第1课时 一元一次方程课件
设这件衣服的原价为x元，可列出方程 。
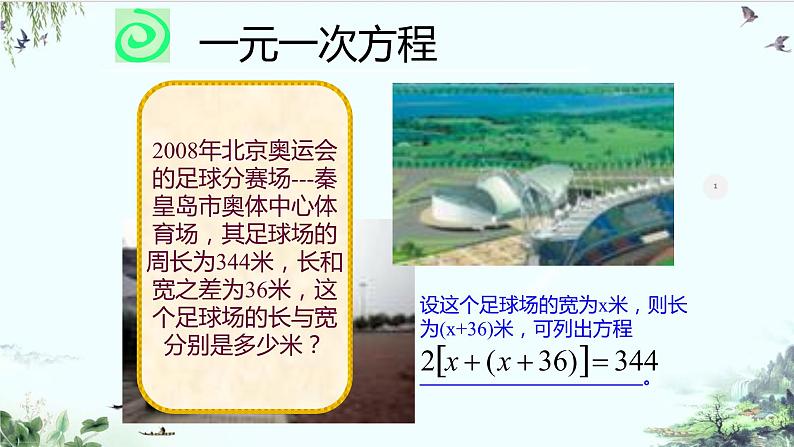
2008年北京奥运会的足球分赛场---秦皇岛市奥体中心体育场，其足球场的周长为344米，长和宽之差为36米，这个足球场的长与宽分别是多少米？
设这个足球场的宽为x米，则长为(x+36)米，可列出方程 。
刚才列的方程,有什么特点？
只含有一个未知数,
等号两边都是整式，这样的方程叫做一元一次方程.
下列哪些是一元一次方程？（1） ； （2） ； （3） ；（4） ；（5） ；（6） ．（7）
智力闯关,谁是英雄
第一关: 是一元一次方程,则k=______;
第二关: 是一元一次方程,则k=______;
第三关 : 是一元一次方程,则k=__ ;
第四关: 是一元一次方程,则k =____.
对于方程4χ=24，容易知道χ=6可以使等式成立， 对于方程1 700+150χ=2 450，你知道χ等于什么时，等式成立？我们来试一试.
我们知道当x=5时，1 700+150x的值是2 450，所以方程1 700+150x=2 450中的未知数的值应是5．
使方程左右两边相等的未知数的值叫方程的解。求方程解的过程叫做解方程。
X=3是方程2x-2=x+1的解吗?　　　　　
１.将数值代入方程左边进行计算，
２.将数值代入方程右边进行计算，
３. 若左边＝右边，则是方程的解，反之，则不是．
χ=2000是方程0.52χ -（1-0.52）χ=80的解吗？
检验一个数值是不是方程的解的步骤：
2、方程(a+6)x2 +3x-8=7是关于x的一元一次方程，则a= _____。
3、一元一次方程2x－3=5的解是（ ） A、4 B、5 C、6 D、7
1、方程 是一元一次方程，则3a-3=_____.
（1）环形跑道一周长400m，沿跑道跑多少周，可以跑3000m？（2）甲种铅笔每枝0.3元，乙种铅笔每枝0.6元，用9元钱买了两种铅笔共20枝，两种铅笔各买了多少枝？（3）一个梯形的下底比上底多2㎝，高是5㎝，面积是40㎝2，求上底。
解：（1） 设跑x周． 列方程 400x=3000
（2）设甲种铅笔买了x枝，乙种铅笔买了（20－x）枝． 列方程 0.3x+0.6（20－x）=9
根据下列问题，设未知数，列出方程。
分析实际问题中的数量关系，利用其中相等关系列出方程，是用数学方法解决实际问题的一种方法。
达标检测 反思目标
1.下列条件中，能列出方程的是：（ ） A．一个数的是3； B.x与-2的差的一半 C.x与y的和的50%； D.甲数的3倍与乙数的的和2.x=3是下列哪个方程的解 （ ） A. 2x+6=0 B.4x=10-x C.5(x-3)=0 D.2x-7=12 3.若2x+1与x－4互为相反数，则可得方程： ________________________.4.某数χ的相反数比它的2倍大1，求某数。 列方程 为：___________________. 5. 有一棵树，刚移栽时，树高为2m，假设以后平均每 年长0.3m，几年后树高为5m？ 解：设x年后树高为5m，可列出方程 _