2022高考物理一轮复习学案 009追及相遇模型+图像法 精讲精练

一.模型及图像特征

1.追及相遇问题中的一个条件和两个关系

(1)一个条件：即两者速度相等，往往是物体能追上、追不上或两者距离最大、最小的临界条件，也是分析判断的切入点。

(2)两个关系：即时间关系和位移关系，这两个关系可通过画过程示意图得到。

2．追及相遇问题的两种典型情况

(1)速度小者追速度大者

(2)速度大者追速度小者

3.追及相遇问题的解题思路及技巧

(1)解题思路

(2)解题技巧

①紧抓“一图三式”，即：过程示意图，时间关系式、速度关系式和位移关系式。

②审题应抓住题目中的关键字眼，充分挖掘题目中的隐含条件，如“刚好”“恰好”“最多”“至少”等，往往对应一个临界状态，满足相应的临界条件。

③若被追的物体做匀减速直线运动，一定要注意追上前该物体是否已经停止运动，另外还要注意最后对解进行讨论分析。

④紧紧抓住速度相等这个临界点。

⑤遇到此类选择题时，图像法往往是最便捷的解法。

二.例题精讲：

例1. 红球匀速运动，速度 V1=8m/s；蓝球匀减速运动直到静止不再运动，初速度V0=12m/s，加速度 a=-1m/s2，蓝球与红球在同一位置同时出发,经多长时间与红球同速?同速前，两者距离如何变化？何时相遇？相遇前何时相距最远？

答案：4s,增大，8s,4s

变式1：红球匀速运动，初速度 V1=8m/s；蓝球匀减速运动直到静止不再运动，初速度V0=12m/s，加速度 a=-1m/s2，蓝球在红球后8m,经多长时间与红球同速?何时相遇？还能再次相遇吗？

答案：4s,4s第一次相遇，不能再次相遇。

变式2：红球匀速运动，速度 V1=8m/s；蓝球匀减速运动直到静止不再运动，初速度V0=12m/s，加速度 a=-1m/s2，蓝球在红球后10m,经多长时间与红球同速? 能相遇吗？何时最近？

答案：4s，不能相遇，4s

变式3：红球匀速运动，速度 V1=8m/s；蓝球匀减速运动直到静止不再运动，初速度V0=12m/s，加速度 a=-1m/s2，蓝球在红球后6m,两球何时同速? 何时相遇？两球距离是怎样变化的？

答案：4s，2s和6s，两次相遇之间，距离先增大后减小，同速时相距最远

变式4：红球匀速运动，速度 V1=4m/s；蓝球匀减速运动直到静止不再运动，初速度V0=12m/s，加速度 a=-1m/s2，蓝球在红球后14m,两球何时同速? 何时相遇？

答案：8s，2s和14.5s

变式5：红球匀速运动，速度 V1=4m/s；蓝球匀减速运动直到静止后立即反向加速，初速度V0=12m/s，加速度 大小始终为1m/s2。蓝球在红球后14m,两球何时同速? 何时相遇？

答案：8s，2s和14s

注意事项：

减速运动分为不可返回和可返回减速运动，对于不可返回运动，要先计算减速到0所需的时间。

例2　一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以a＝3 m/s2的加速度开始行驶，恰在这一时刻一辆自行车以v自＝6 m/s的速度匀速驶来，从旁边超过汽车。试求：

(1)汽车从路口开动后，在追上自行车之前经过多长时间两车相距最远？此时距离是多少？

(2)什么时候汽车能追上自行车？此时汽车的速度是多少？

答案：　(1)2_s__6_m__(2)4_s__12_m/s

(1)解法一(物理分析法)：

如图甲所示，汽车与自行车的速度相等时相距最远，设此时经过的时间为t1，汽车和自行车间的距离为Δx，则有v自＝at1

所以t1＝＝2 s

Δx＝v自t1－at＝6 m。

解法二(相对运动法)：

以自行车为参考系，则从开始到相距最远的这段时间内，汽车相对这个参考系的各个物理量为

初速度v0＝v汽初－v自＝0－6 m/s＝－6 m/s

末速度vt＝v汽末－v自＝0

加速度a′＝a－a自＝3 m/s2－0＝3 m/s2

所以汽车和自行车相距最远时经历的时间为

t1＝＝2 s

最大相对位移Δx＝＝－6 m

负号表示汽车在后。

注意：利用相对运动的方法解题，要抓住三个关键：①选取哪个物体为研究对象；②选取哪个物体为参考系；③规定哪个方向为正方向。

解法三(极值法)：

设汽车在追上自行车之前经过时间t1汽车和自行车相距Δx，则Δx＝v自t1－at

代入已知数据得Δx＝6t1－t

由二次函数求极值的条件知：t1＝2 s时，Δx有最大值6 m。

所以经过t1＝2 s后，汽车和自行车相距最远，最远距离为Δx＝6 m。

解法四(图像法)：

自行车和汽车的v­t图像如图乙所示。由图可以看出，在相遇前，t1时刻汽车和自行车速度相等，相距最远，此时的距离为阴影三角形的面积，所以有

t1＝＝ s＝2 s

Δx＝＝ m＝6 m。

(2)解法一(物理分析法)：

当汽车和自行车位移相等时，汽车追上自行车，设此时经过的时间为t2，则有v自t2＝at

解得t2＝＝ s＝4 s

此时汽车的速度v1′＝at2＝12 m/s。

解法二(图像法)：

由前面画出的v ­t图像可以看出，在t1时刻之后，当由图线v自、v汽和t＝t2构成的三角形的面积与阴影部分的三角形面积相等时，汽车与自行车的位移相等

三.举一反三，巩固练习

1. (2018·全国卷Ⅱ)(多选)甲、乙两汽车在同一条平直公路上同向运动，其速度—时间图像分别如图中甲、乙两条曲线所示。已知两车在t2时刻并排行驶，下列说法正确的是(　　)

A．两车在t1时刻也并排行驶

B．t1时刻甲车在后，乙车在前

C．甲车的加速度大小先增大后减小

D．乙车的加速度大小先减小后增大

2. (2018·全国卷Ⅲ)(多选)甲、乙两车在同一平直公路上同向运动，甲做匀加速直线运动，乙做匀速直线运动。甲、乙两车的位置x随时间t的变化如图所示。下列说法正确的是(　　)

A．在t1时刻两车速度相等

B．从0到t1时间内，两车走过的路程相等

C．从t1到t2时间内，两车走过的路程相等

D．从t1到t2时间内的某时刻，两车速度相等

3.制动防抱死系统(antilock brake system)简称ABS，其作用就是在汽车制动时，自动控制制动器制动力的大小，使车轮不被抱死，处于边滚边滑的状态，以保证车轮与地面的附着力为最大值。某汽车在启用ABS刹车系统和不启用该刹车系统紧急刹车时，其车速随时间的变化关系分别如图中的①、②图线所示。由图可知，启用ABS后(　　)

A．瞬时速度总比不启用ABS时小

B．加速度总比不启用ABS时大

C．刹车后的平均速度比不启用ABS时小

D．刹车后前行的距离比不启用ABS更短

4．如图所示，图甲为质点a和b做直线运动的位移—时间图像，图乙为质点c和d做直线运动的速度—时间图像，由图可知(　　)

A．若t1时刻a、b两质点第一次相遇，则t2时刻两质点第二次相遇

B．若t1时刻c、d两质点第一次相遇，则t2时刻两质点第二次相遇

C．t1到t2时间内，b和d两个质点的运动方向发生了改变

D．t1到t2时间内，a和d两个质点的速率先减小后增大

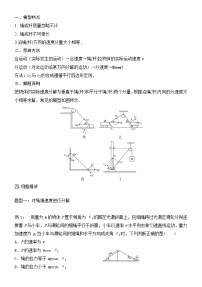
5.a、b两车在平直公路上沿同一方向行驶，两车运动的v­t图像如图所示，在t＝0时刻，b车在a车前方s0处，在0～t1时间内，a车的位移为s。若s＝2s0，则(　　)

A．a、b两车只会相遇一次，在t1时刻相遇

B．a、b两车只会相遇一次，在时刻相遇

C．a、b两车可以相遇两次，一次在时刻相遇，另一次在时刻相遇

D．a、b两车可以相遇两次，一次在时刻相遇，另一次在时刻相遇

6．在一大雾天，一辆小汽车以30 m/s的速度行驶在高速公路上，突然发现正前方30 m处有一辆大卡车以10 m/s的速度同方向匀速行驶，小汽车紧急刹车，刹车过程中刹车失灵．如图a、b分别为小汽车和大卡车的v－t图象，以下说法正确的是(　　)

A．因刹车失灵前小汽车已减速，不会追尾

B．在t＝5 s时追尾

C．在t＝3 s时追尾

D．由于初始距离太近，即使刹车不失灵也会追尾

7．如图所示，A、B两物体相距s＝7 m时，A在水平拉力和摩擦力作用下，正以vA＝4 m/s的速度向右匀速运动，而物体B此时正以vB＝10 m/s向右匀减速运动，加速度a＝－2 m/s2，则A追上B所经历时间是(　　)

A．7 s   B．8 s 

C．9 s   D．10 s

8.　(2020·安徽省定远重点中学高三3月线上模拟)(多选)甲、乙两辆小汽车(都可视为质点)分别处于同一条平直公路的两条平行车道上，开始时(t＝0)乙车在前甲车在后，两车间距为x0，t＝0时甲车先启动，t＝3 s时乙车再启动，两车启动后都是先做匀加速运动，后做匀速运动，v­t图像如图所示。根据图像，下列说法正确的是(　　)

A．两车加速过程，甲的加速度比乙大

B．若x0＝80 m，则两车间距最小为30 m

C．若两车在t＝5 s时相遇，则在t＝9 s时再次相遇

D．若两车在t＝4 s时相遇，则在t＝10 s时再次相遇

9.

2012年10月4日，云南省彝良县发生特大泥石流．如右图所示，一汽车停在小山坡底，突然司机发现在距坡底240 m的山坡处泥石流以8 m/s的初速度、0.4 m/s2的加速度匀加速倾泄而下，假设泥石流到达坡底后速率不变，在水平地面上做匀速直线运动．已知司机的反应时间为1 s，汽车启动后以0.5 m/s2的加速度一直做匀加速直线运动．试分析汽车能否安全脱离？

 10　.一辆卡车以vB＝10 m/s的初速度沿直线方向做匀减速直线运动，加速度的大小为a＝2 m/s2，在其后方一辆小汽车以vA＝4 m/s的速度向相同方向做匀速直线运动，小汽车在卡车后方相距x0＝7 m处，从此时开始计时，求：

(1)小汽车追上卡车前，两车间的最大距离d是多大？

(2)经过多长时间小汽车追上卡车？

四.举一反三，巩固练习参考答案：

1. (2018·全国卷Ⅱ)(多选)甲、乙两汽车在同一条平直公路上同向运动，其速度—时间图像分别如图中甲、乙两条曲线所示。已知两车在t2时刻并排行驶，下列说法正确的是(　　)

A．两车在t1时刻也并排行驶

B．t1时刻甲车在后，乙车在前

C．甲车的加速度大小先增大后减小

D．乙车的加速度大小先减小后增大

答案　BD

解析　v­t图像中图像与t轴所包围的面积代表运动的位移，两车在t2时刻并排行驶，利用逆向思维并借助于面积可知在t1时刻甲车在后，乙车在前，故A错误，B正确；图像的斜率表示加速度，所以甲的加速度先减小后增大，乙的加速度也是先减小后增大，故C错误，D正确。

2. (2018·全国卷Ⅲ)(多选)甲、乙两车在同一平直公路上同向运动，甲做匀加速直线运动，乙做匀速直线运动。甲、乙两车的位置x随时间t的变化如图所示。下列说法正确的是(　　)

A．在t1时刻两车速度相等

B．从0到t1时间内，两车走过的路程相等

C．从t1到t2时间内，两车走过的路程相等

D．从t1到t2时间内的某时刻，两车速度相等

答案　CD

解析　根据位移—时间图像的物理意义可知，在t1时刻两车的位置相同，速度不相等，乙车的速度大于甲车的速度，A错误；从0到t1时间内，乙车走过的路程大于甲车，B错误；从t1到t2时间内，两车都是从x1位置走到x2位置，两车走过的路程相等，C正确；根据位移—时间图像的斜率等于速度可知，从t1到t2时间内的某时刻，有甲图线的切线与乙图线平行、斜率相同，两车速度相等，D正确。

3.制动防抱死系统(antilock brake system)简称ABS，其作用就是在汽车制动时，自动控制制动器制动力的大小，使车轮不被抱死，处于边滚边滑的状态，以保证车轮与地面的附着力为最大值。某汽车在启用ABS刹车系统和不启用该刹车系统紧急刹车时，其车速随时间的变化关系分别如图中的①、②图线所示。由图可知，启用ABS后(　　)

A．瞬时速度总比不启用ABS时小

B．加速度总比不启用ABS时大

C．刹车后的平均速度比不启用ABS时小

D．刹车后前行的距离比不启用ABS更短

答案　D

解析　v­t图像中各点的纵坐标表示对应的速度，由图可知，启用ABS后，瞬时速度开始时比不启用时要大，故A错误；v­t图像的斜率表示加速度，由图可知，启用ABS后，开始时的加速度小于不启用时的加速度，故B错误；由图可知，启用ABS后经过的位移明显小于不启用时的位移，但由于时间关系不明显，故无法比较两种情况下的平均速度大小，故C错误，D正确。

4．如图所示，图甲为质点a和b做直线运动的位移—时间图像，图乙为质点c和d做直线运动的速度—时间图像，由图可知(　　)

A．若t1时刻a、b两质点第一次相遇，则t2时刻两质点第二次相遇

B．若t1时刻c、d两质点第一次相遇，则t2时刻两质点第二次相遇

C．t1到t2时间内，b和d两个质点的运动方向发生了改变

D．t1到t2时间内，a和d两个质点的速率先减小后增大

答案　A

解析　在x­t图像中，两图线的交点表示两质点位置相同即相遇，由图甲可知，若t1时刻a、b两质点第一次相遇，则t2时刻两质点第二次相遇，故A正确；根据v­t图像与t轴所围成的面积表示位移知，t1到t2时间内，c的位移大于d的位移，若t1时刻c、d两质点第一次相遇，则t2时刻两质点没有相遇，故B错误；根据图甲、乙可知，只有质点b运动方向改变，质点a、c、d的运动方向未发生改变，故C错误；根据x­t图像知，t1到t2时间内，a

质点的速度不变，由v­t图像知，t1到t2时间内，d的速率先减小后增大，故D错误。

5.a、b两车在平直公路上沿同一方向行驶，两车运动的v­t图像如图所示，在t＝0时刻，b车在a车前方s0处，在0～t1时间内，a车的位移为s。若s＝2s0，则(　　)

A．a、b两车只会相遇一次，在t1时刻相遇

B．a、b两车只会相遇一次，在时刻相遇

C．a、b两车可以相遇两次，一次在时刻相遇，另一次在时刻相遇

D．a、b两车可以相遇两次，一次在时刻相遇，另一次在时刻相遇

答案　D

解析　由v­t图像与时间轴围成的面积表示位移可知，s＝t1＝，s0＝＝。t1时刻两车的位移差为Δs＝t1＝vt1>s0，则由题设可知，a、b两车可以相遇两次。设第一次相遇的时刻为t0，则＝2，解得t0＝，根据对称性，另一次在时刻相遇。故A、B、C错误，D正确。

6．在一大雾天，一辆小汽车以30 m/s的速度行驶在高速公路上，突然发现正前方30 m处有一辆大卡车以10 m/s的速度同方向匀速行驶，小汽车紧急刹车，刹车过程中刹车失灵．如图a、b分别为小汽车和大卡车的v－t图象，以下说法正确的是(　　)

A．因刹车失灵前小汽车已减速，不会追尾

B．在t＝5 s时追尾

C．在t＝3 s时追尾

D．由于初始距离太近，即使刹车不失灵也会追尾

解析：根据速度图象与横轴所围面积等于位移可知，两车速度相等时(t＝5 s)小汽车相对于大卡车位移为35 m，所以会追尾，选项A错误；在t＝3 s时，小汽车相对于大卡车位移等于30 m，发生追尾，选项C正确，B错误；若刹车不失灵，在t＝2 s时两车速度相等，小汽车相对于大卡车位移等于20 m，小于开始时的30 m距离，所以刹车不失灵不会追尾，选项D错误．

答案：C

7．如图所示，A、B两物体相距s＝7 m时，A在水平拉力和摩擦力作用下，正以vA＝4 m/s的速度向右匀速运动，而物体B此时正以vB＝10 m/s向右匀减速运动，加速度a＝－2 m/s2，则A追上B所经历时间是(　　)

A．7 s   B．8 s 

C．9 s   D．10 s

解析：由题意知，t＝5 s时，物体B的速度减为零，位移大小xB＝at2＝25 m，此时A的位移xA＝vAt＝20 m，A、B两物体相距Δs＝s＋xB－xA＝7 m＋25 m－20 m＝12 m，再经过Δt＝Δs/vA＝3 s，A追上B，所以A追上B所经历时间是5 s＋3 s＝8 s，选项B正确．

答案：B

8.　(2020·安徽省定远重点中学高三3月线上模拟)(多选)甲、乙两辆小汽车(都可视为质点)分别处于同一条平直公路的两条平行车道上，开始时(t＝0)乙车在前甲车在后，两车间距为x0，t＝0时甲车先启动，t＝3 s时乙车再启动，两车启动后都是先做匀加速运动，后做匀速运动，v­t图像如图所示。根据图像，下列说法正确的是(　　)

A．两车加速过程，甲的加速度比乙大

B．若x0＝80 m，则两车间距最小为30 m

C．若两车在t＝5 s时相遇，则在t＝9 s时再次相遇

D．若两车在t＝4 s时相遇，则在t＝10 s时再次相遇

答案　BC

解析　v­t图像的斜率表示加速度，则从图像上可以看出，两车加速过程，乙的加速度比甲大，故A错误；速度相等时两车间距有最小值，从图像上可以看出t＝7 s时，两车速度相等，此时甲运动的位移为x1＝ m＝90 m，乙运动的位移为x2＝×4×20 m＝40 m，则此时甲、乙之间的距离为Δx＝x2＋x0－x1＝30 m，故B正确；若两车在t＝5 s时相遇，从图像上可以看出5～9 s内甲、乙运动的位移相等，所以甲、乙在t＝9 s时会再次相遇，故C正确；若两车在t＝4 s时相遇，从图像上可以看出4～10 s内甲、乙运动的位移不相等，则在t＝10 s时两车不会再次相遇，故D错误。

9.

2012年10月4日，云南省彝良县发生特大泥石流．如右图所示，一汽车停在小山坡底，突然司机发现在距坡底240 m的山坡处泥石流以8 m/s的初速度、0.4 m/s2的加速度匀加速倾泄而下，假设泥石流到达坡底后速率不变，在水平地面上做匀速直线运动．已知司机的反应时间为1 s，汽车启动后以0.5 m/s2的加速度一直做匀加速直线运动．试分析汽车能否安全脱离？

解析：设泥石流到达坡底的时间为t1，速率为v1，

则x1＝v0t1＋a1t，v1＝v0＋a1t1

代入数据得t1＝20 s，v1＝16 m/s

而汽车在t2＝19 s的时间内发生位移为x2＝a2t＝90.25 m，速度为v2＝a2t2＝9.5 m/s

令再经时间t3，泥石流追上汽车，则有

v1t3＝x2＋v2t3＋a2t

代入数据并化简得t－26t3＋361＝0，因Δ<0，方程无解．

所以泥石流无法追上汽车，汽车能完全脱离．

答案：见解析

 10　.一辆卡车以vB＝10 m/s的初速度沿直线方向做匀减速直线运动，加速度的大小为a＝2 m/s2，在其后方一辆小汽车以vA＝4 m/s的速度向相同方向做匀速直线运动，小汽车在卡车后方相距x0＝7 m处，从此时开始计时，求：

(1)小汽车追上卡车前，两车间的最大距离d是多大？

(2)经过多长时间小汽车追上卡车？

答案　(1)16 m　(2)8 s

解析　(1)设两车速度相等经历的时间为t1，有：

vA＝vB－at1，

卡车做匀减速直线运动，有：v－v＝－2axB1，

小汽车做匀速直线运动，有：xA1＝vAt1，

两者间的最大距离为：d＝x0＋xB1－xA1，

联立以上各式并代入数据解得：d＝16 m。

(2)设卡车速度减为零的时间为t2，有：0＝vB－at2，

解得：t2＝5 s，

设卡车速度减为零的位移为xB，有：2axB＝v，

解得：xB＝25 m，

此时小汽车的位移为：xA＝vAt2＝4×5 m＝20 m

因为xA＜xB＋x0，可知卡车速度减为零时，小汽车还未追上卡车。

还需追及的时间为：

t3＝＝ s＝3 s，

则小汽车追上卡车经过的时间为：

t＝t2＋t3＝5 s＋3 s＝8 s。