初中数学北师大版八年级上册1 函数学案

这是一份初中数学北师大版八年级上册1 函数学案，共8页。
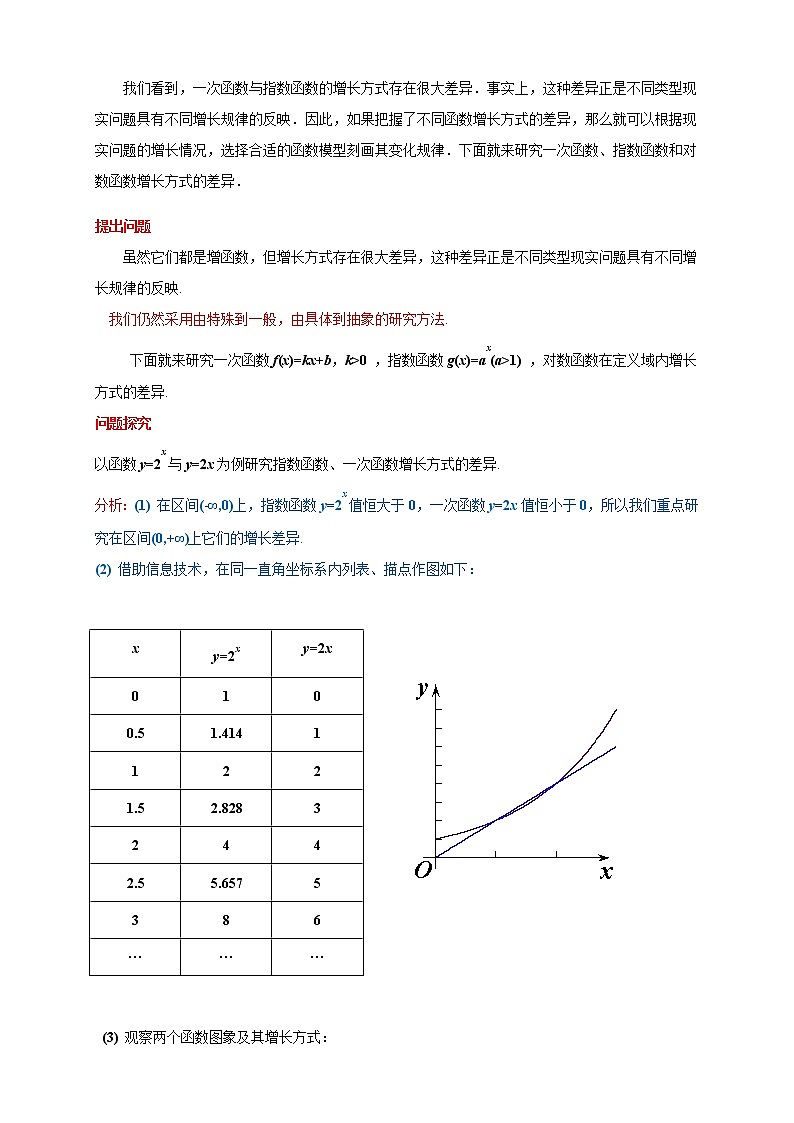
第四章  指数函数与对数函数4.4.3 不同增长函数的差异1.了解指数函数、对数函数、线性函数 (一次函数) 的增长差异.2.理解对数增长、直线上升、指数爆炸。重点：函数增长快慢比较的常用方法；难点：了解影响函数增长快慢的因素；三种函数模型的性质 y＝ax(a>1)y＝logax(a>1)y＝xn(n>0)在(0，＋∞)上的增减性增函数增函数增函数图象的变化趋势随x增大逐渐近似与y轴——平行随x增大逐渐近似与x——轴平行随n值而不同增长速度①y＝ax(a>1)：随着x的增大，y增长速度越来越快，会远远大于y＝xn(n>0)的增长速度，y＝logax(a>1)的增长速度越来越慢②存在一个x0，当x>x0时，有ax>x——n>logx增函数;增函数;增函数;y轴;x轴;越来越快;越来越慢;ax>xn>logax我们看到，一次函数与指数函数的增长方式存在很大差异．事实上，这种差异正是不同类型现实问题具有不同增长规律的反映．因此，如果把握了不同函数增长方式的差异，那么就可以根据现实问题的增长情况，选择合适的函数模型刻画其变化规律．下面就来研究一次函数、指数函数和对数函数增长方式的差异．提出问题    虽然它们都是增函数，但增长方式存在很大差异，这种差异正是不同类型现实问题具有不同增长规律的反映.我们仍然采用由特殊到一般，由具体到抽象的研究方法.下面就来研究一次函数f(x)=kx+b，k>0 ，指数函数g(x)=ax(a>1) ，对数函数在定义域内增长方式的差异.                   问题探究以函数y=2x与y=2x为例研究指数函数、一次函数增长方式的差异.              分析：(1) 在区间(-∞,0)上，指数函数y=2x值恒大于0，一次函数y=2x值恒小于0，所以我们重点研究在区间(0,+∞)上它们的增长差异.(2) 借助信息技术，在同一直角坐标系内列表、描点作图如下：xy=2xy=2x0100.51.41411221.52.82832442.55.6575386·········  (3) 观察两个函数图象及其增长方式：结论1：函数y=2x与y=2x有两个交点(1,2)和(2,4)结论2：在区间(0,1)上，函数y=2x的图象位于y=2x之上结论3：在区间(1,2)上，函数y=2x的图象位于y=2x之下结论4：在区间(2,3)上，函数y=2x的图象位于y=2x之上综上：虽然函数y=2x与y=2x都是增函数，但是它们的增长速度不同，函数y=2x的增长速度不变，但是y=2x的增长速度改变，先慢后快.请大家想象一下，取更大的x值，在更大的范围内两个函数图象的关系？思考：随着自变量取值越来越大，函数y=2x的图象几乎与x轴垂直，函数值快速增长，函数y=2x的增长速度保持不变，和y=2x的增长相比几乎微不足道.     归纳总结总结一：函数y=2x与y=2x在[0,+∞)上增长快慢的不同如下：虽然函数y=2x与y=2x在[0,+∞)上都是单调递增，但它们的增长速度不同.随着x的增大，y=2x的增长速度越来越快，会超过并远远大于  y=2x的增长速度.尽管在x的一定范围内，2x<2x，但由于y=2x的增长最终会快于y=2x的增长，因此，总会存在一个x0，当x>x0时，恒有2x>2x.总结二：一般地指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长都与上述类似.即使k值远远大于a值，指数函数y=ax(a>1)虽然有一段区间会小于y=kx(k>0)，但总会存在一个x0，当x>x0时， y=ax(a>1)的增长速度会大大超过y=kx(k>0)的增长速度.跟踪训练1．四个变量y1，y2，y3，y4随变量x变化的数据如表：x151015202530y1226101226401626901y22321 02437 7681.05×1063.36×1071.07×109y32102030405060y424.3225.3225.9076.3226.6446.907关于x呈指数函数变化的变量是________. 答案：y2　[以爆炸式增长的变量呈指数函数变化．从表格中可以看出，四个变量y1，y2，y3，y4均是从2开始变化，且都是越来越大，但是增长速度不同，其中变量y2的增长速度最快，画出它们的图象(图略)，可知变量y2关于x呈指数型函数变化．故填y2.]分析：(1) 在区间(-∞,0)上，对数函数y=lgx没意义，一次函数值恒小于0，所以研究在区间(0,+∞)上它们的增长差异.(2) 借助信息技术，在同一直角坐标系内列表、描点作图如下：xy=lgx 0不存在01011201.3012301.4773401.6024501.6995601.7786·········以函数y=lgx与 为例研究对数函数、一次函数增长方式的差异.               (3) 观察两个函数图象及其增长方式：总结一：虽然函数y=lgx与 在(0,+∞)上都是单调递增，但它们的增长速度存在明显差异. 在(0,+∞)上增长速度不变，y=lgx在(0,+∞)上的增长速度在变化.随着x的增大，         的图象离x轴越来越远，而函数y=lgx的图象越来越平缓，就像与x轴平行一样.例如：lg10=1，lg100=2，lg1000=3，lg10000=4；这表明，当x>10，即y>1，y=lgx比    相比增长得就很慢了.思考：将y=lgx放大1000倍，将函数y=1000lgx与比较，仍有上面规律吗？先想象一下，仍然有.总结二：一般地，虽然对数函数                与一次函数y=kx(k>0)在(0,上都是单调递增，但它们的增长速度不同.随着x的增大，一次函数y=kx(k>0)保持固定的增长速度，而对数函数               的增长速度越来越慢.不论a值比k值大多少，在一定范围内，可能会大于kx，但由于         的增长会慢于kx的增长，因此总存在一个x0，当x>x0时，恒有． 跟踪训练1．函数f(x)＝lg x，g(x)＝0.3x－1的图象如图所示． (1)试根据函数的增长差异指出曲线C1，C2分别对应的函数；(2)比较两函数的增长差异(以两图象交点为分界点，对f(x)，g(x)的大小进行比较). [解]　(1)C1对应的函数为g(x)＝0.3x－1，C2对应的函数为f(x)＝lg x.(2)当x<x1时，g(x)>f(x)；当x1<x<x2时，f(x)>g(x)；当x>x2时，g(x)>f(x)；当x＝x1或x＝x2时，f(x)＝g(x)．1．下列函数中随x的增大而增大且速度最快的是(　　)A．y＝ex　 B．y＝ln xC．y＝x2   D．y＝e－x【答案】A　[结合指数函数，对数函数及一次函数的图象变化趋势可知A正确．]2．能使不等式log2x<x2<2x一定成立的x的取值区间是(　　)A．(0，＋∞)   B．(2，＋∞)C．(－∞，2)   D．(4，＋∞)【答案】D　[当x>4时，log2x<x2<2x，故选D.]3．某工厂8年来某种产品总产量C与时间t(年)的函数关系如图所示． 以下四种说法：①前三年产量增长的速度越来越快；②前三年产量增长的速度越来越慢；③第三年后这种产品停止生产；④第三年后产量保持不变．其中说法正确的序号是________.  【答案】②④　[结合图象可知②④正确，故填②④.]4．某人投资x元，获利y元，有以下三种方案．甲：y＝0.2x，乙：y＝log2x＋100，丙：y＝1.005x，则投资500元，1 000元，1 500元时，应分别选择________方案. 【答案】乙、甲、丙　[将投资数分别代入甲、乙、丙的函数关系式中比较y值的大小即可求出．]1.由特殊到一般，由具体到抽象研究了一次函数f(x)=kx+b，k>0，指数 函数g(x)=ax(a>1) ，对数函数                在定义域上的不同增长方式.2.根据图象判断增长型的指数函数、对数函数和幂函数时，通常是观察函数图象上升得快慢，即随着自变量的增大，图象最“陡”的函数是指数函数；图象趋于平缓的函数是对数函数．